题目内容
(2005 北京东城)如图所示,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.
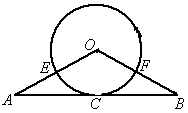
(1)求证AB是⊙O的切线;
(2)若△ABO腰上的高等于底边的一半,且 ,求
,求 的长.
的长.
答案:略
解析:
提示:
解析:
|
解 (1)证明 如图
连接OC. ∵OA=OB,AC=BC, ∴OC⊥AB. 故AB是⊙O的切线. (2) 过B点作BD⊥AO,交AO延长线于D点,由题意有AB=2BD,由题目条件,有 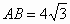 . .
在直角三角形 ABD中,根据正弦定义 . .
∴∠ A=30°.在直角三角形 ACO中,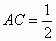 , ,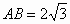 ,∠A=30°,则AO=2OC. ,∠A=30°,则AO=2OC.
由勾股定理,求得 OC=2.∵ OA=OB,且∠A=30°,∴∠AOB=120°.由弧长公式可求得 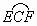 的长为 的长为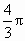 . . |
提示:
|
点评 本题是一道圆与三角形相结合的综合题目,涉及到圆的切线、直角三角形、勾股定理、三角函数的定义等多方面的知识,运用了数形结合的思想.考查范围广,是一道体现学生知识能力水平高低的好题. |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目

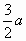
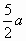
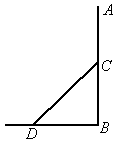
 .
. 与x轴交于整数点,求m的值;
与x轴交于整数点,求m的值;