题目内容
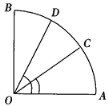
【题目】已知:如图,∠AOB=90°,AO=OB,C、D是弧AB上的两点,∠AOD>∠AOC,
(1)0<sin∠AOC<sin∠AOD<1;
(2)1>cos∠AOC>cos∠AOD>0;
(3)锐角的正弦函数值随角度的增大而______;
(4)锐角的余弦函数值随角度的增大而______.
【答案】(1)见解析(2)见详解;(3)增大;(4)减小.
【解析】
第(1)(2)问作辅助线,分别在Rt△OEC和Rt△DFO中利用三角函数定义表示出所求三角函数,再利用不等式的性质:不等号两边同时除以同一个不为零的正数时不等号仍成立即可解题;第(3)(4)两问根据特殊三角函数值,总结规律即可解题.
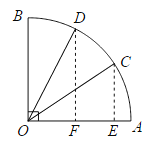
解:(1)如图所示,作CE⊥OA与E,作DF⊥OA与F.
∵sin∠AOC=![]() , sin∠AOD=
, sin∠AOD=![]() ,
,![]() ,
,
∴0<sin∠AOC<sin∠AOD<1;(不等式性质)
(2)∵cos∠AOC=![]() , cos∠AOD=
, cos∠AOD=![]() ,
,![]() ,
,
∴1>cos∠AOC>cos∠AOD>0;(不等式性质)
(3)由特殊的直角三角函数值,总结规律,即可发现对于锐角而言, 锐角的正弦函数值随角度的增大而增大;
(4)由特殊的直角三角函数值,总结规律,即可发现对于锐角而言, 锐角的余弦函数值随角度的增大而减小.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目