Question

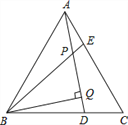
【题目】已知，如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于点P，下列说法：①∠APE=∠C，② AQ=BQ，③BP=2PQ, ④AE+BD=AB，其正确的个数有（ ）个．

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】试题解析：∵△ABC是等边三角形，

∴AB=AC，∠BAE=∠C=60°，

在△ABE和△CAD中，

AB＝AC，∠BAE＝∠C，AE＝CD，

∴△ABE≌△CAD（SAS）.

∴∠ABE =∠CAD，

∴∠BPQ=∠ABE +∠BAP=∠CAD +∠BAP =∠BAC=60°，

∴∠APE=∠BPQ=60°，

∴∠APE=∠C.

故①结论正确；

∵BQ⊥AD，

∴∠PBQ=90°-∠BPQ=90°-60°=30°，

∴BP=2PQ．

故③结论正确；

∵△ABE≌△CAD，

∴AE=CD，

∴AE+BD=CD+BD=BC=AB.

故④结论正确；

无法证明AQ=BQ成立，故②结论错误.

故选C．