题目内容
(2012•汕头模拟)如图,直角梯形OABC的一顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上,OA∥BC,D是BC上一点,BD=
OA=
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.

(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,求y的值.
| 1 |
| 4 |
| 2 |

(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,求y的值.
分析:(1)过点B作BF⊥OA于F,由∠OAB=45°,AB=3,即可求得BF与AF的值,又由BD=
OA=
,即可求得CD的长,则可求得D点的坐标;
(2)首先连接OD,由结论(1)知:D在∠COA的平分线上,可得∠DOE=∠COD=45°,又由∠1=∠2,可判定△ODE∽△AEF,根据相似三角形的对应边成比例,即可得到y与x之间的函数关系;
(3)当△AEF为等腰三角形时,存在EF=AE或AF=AE或EF=AF共3种情况,分别从这三种情况去分析,利用相似三角形的性质,等腰直角三角形的性质以及矩形的性质求解,即可求得答案.
| 1 |
| 4 |
| 2 |
(2)首先连接OD,由结论(1)知:D在∠COA的平分线上,可得∠DOE=∠COD=45°,又由∠1=∠2,可判定△ODE∽△AEF,根据相似三角形的对应边成比例,即可得到y与x之间的函数关系;
(3)当△AEF为等腰三角形时,存在EF=AE或AF=AE或EF=AF共3种情况,分别从这三种情况去分析,利用相似三角形的性质,等腰直角三角形的性质以及矩形的性质求解,即可求得答案.
解答: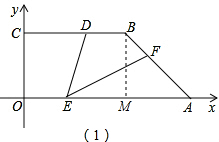 解:(1)如图(1),过点B作BM⊥OA于M,
解:(1)如图(1),过点B作BM⊥OA于M,
∵∠OAB=45°,
∴AM=BM=AB•sin∠OAB=3×
=
,
∵BD=
OA=
,
∴OA=4
,
∴CD=BC-BD=OM-BD=4
-
-
=
,
∴D点的坐标是(
,
).(2分)
(2)连接OD,如图(2),由结论(1)知:D在∠COA的平分线上,
则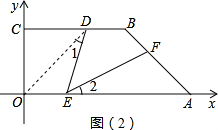 ∠DOE=∠COD=45°,
∠DOE=∠COD=45°,
又∵在梯形DOAB中,∠BAO=45°,
∴OD=AB=3,
由三角形外角定理得:∠1=∠DEA-∠DOE=∠DEA-45°,
又∵∠2=∠DEA-45°,
∴∠1=∠2,
∴△ODE∽△AEF,
∴
=
,
即:
=
∴y与x的解析式为:y=-
x2+
x;(6分)
(3)当△AEF为等腰三角形时,存在EF=AE或AF=AE或EF=AF共3种情况.
①当EF=AE时,如图(3),
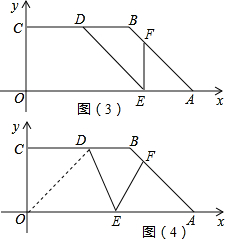 ∴∠EFA=∠DEF=45°,
∴∠EFA=∠DEF=45°,
∴DE∥AB,
又∵DB∥EA,
∴四边形DEAB是平行四边形,
∴AE=DB=
,
∴AF=
AE=2,
∴y=2;
②当AF=AE时,如图(4),连接OD,
由(2)知△ODE∽△AEF,
则
=
,
即
=
,
则3y=4
x-x2,①,
又OE+AE=4
,即x+y=4
②,
联立①②解得:y=4
-3;
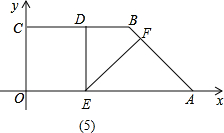 ③当EF=AF时,如图(5).∠FAE=∠FEA=∠DEF=45°,
③当EF=AF时,如图(5).∠FAE=∠FEA=∠DEF=45°,
∴△AEF为等腰直角三角形.
∴∠AEF=45°,
∵∠DEF=45°,
∴∠DEA=90°,
∴四边形COED是矩形,
∴OE=CD=
,
∴AE=4
-
=
,
∴AF=AE•sin45°=
;
∴当△AEF为等腰三角形时,y的值为2或4
-3或
.(12分)
 解:(1)如图(1),过点B作BM⊥OA于M,
解:(1)如图(1),过点B作BM⊥OA于M,∵∠OAB=45°,
∴AM=BM=AB•sin∠OAB=3×
| ||
| 2 |
3
| ||
| 2 |
∵BD=
| 1 |
| 4 |
| 2 |
∴OA=4
| 2 |
∴CD=BC-BD=OM-BD=4
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
∴D点的坐标是(
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
(2)连接OD,如图(2),由结论(1)知:D在∠COA的平分线上,
则
 ∠DOE=∠COD=45°,
∠DOE=∠COD=45°,又∵在梯形DOAB中,∠BAO=45°,
∴OD=AB=3,
由三角形外角定理得:∠1=∠DEA-∠DOE=∠DEA-45°,
又∵∠2=∠DEA-45°,
∴∠1=∠2,
∴△ODE∽△AEF,
∴
| OE |
| AF |
| OD |
| AE |
即:
| x |
| y |
| 3 | ||
4
|
∴y与x的解析式为:y=-
| 1 |
| 3 |
4
| ||
| 3 |
(3)当△AEF为等腰三角形时,存在EF=AE或AF=AE或EF=AF共3种情况.
①当EF=AE时,如图(3),
 ∴∠EFA=∠DEF=45°,
∴∠EFA=∠DEF=45°,∴DE∥AB,
又∵DB∥EA,
∴四边形DEAB是平行四边形,
∴AE=DB=
| 2 |
∴AF=
| 2 |
∴y=2;
②当AF=AE时,如图(4),连接OD,
由(2)知△ODE∽△AEF,
则
| OD |
| AE |
| OE |
| AF |
即
| 3 | ||
4
|
| x |
| y |
则3y=4
| 2 |
又OE+AE=4
| 2 |
| 2 |
联立①②解得:y=4
| 2 |
 ③当EF=AF时,如图(5).∠FAE=∠FEA=∠DEF=45°,
③当EF=AF时,如图(5).∠FAE=∠FEA=∠DEF=45°,∴△AEF为等腰直角三角形.
∴∠AEF=45°,
∵∠DEF=45°,
∴∠DEA=90°,
∴四边形COED是矩形,
∴OE=CD=
| 3 |
| 2 |
| 2 |
∴AE=4
| 2 |
| 3 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
∴AF=AE•sin45°=
| 5 |
| 2 |
∴当△AEF为等腰三角形时,y的值为2或4
| 2 |
| 5 |
| 2 |
点评:此题考查了相似三角形的判定与性质、直角梯形的性质、矩形的判定与性质、等腰直角三角形的性质以及三角函数等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想、方程思想与分类讨论思想的应用,注意准确作出辅助线.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
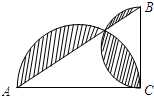 (2012•汕头模拟)如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为( )
(2012•汕头模拟)如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为( )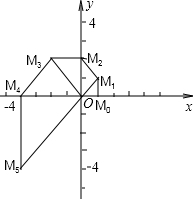 (2012•汕头模拟)如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段OM0绕原点O沿逆时针方向旋转45°,再将其延长到M1,使M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2,使M2M1⊥OM1,得到线段OM2,如此下去,得到线段
(2012•汕头模拟)如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段OM0绕原点O沿逆时针方向旋转45°,再将其延长到M1,使M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2,使M2M1⊥OM1,得到线段OM2,如此下去,得到线段