题目内容
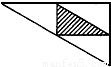
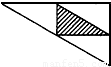
厨房角柜的台面是三角形，如图，如果把各边中点的连线所围成的三角形铺成黑色大理石．（图中阴影部分）其余部分铺成白色大理石，那么黑色大理石的面积与白色大理石面积的比是（ ）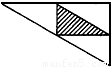
A．
B．
C．
D．
【答案】分析：根据三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．易证明此图中分割的四个三角形的面积都相等．所以黑色大理石的面积与白色大理石面积的比是1：3．
解答：
解：如图，
∵D、E、F分别是AB、BC、AC的中点
∴DF=BE=EC，EF=AD=BD，DE=AF=FC
∴△BDE≌△ADF≌△CEF≌△DEF
∴S△BDE=S△ADF=S△CEF=S△DEF
∴黑色大理石的面积与白色大理石面积的比是1：3．
故选C．
点评：本题构造的问题情境经常考查：根据三角形的中位线定理可以证明三角形被它的三条中位线分成的四个三角形全等．
解答：
解：如图，∵D、E、F分别是AB、BC、AC的中点
∴DF=BE=EC，EF=AD=BD，DE=AF=FC
∴△BDE≌△ADF≌△CEF≌△DEF
∴S△BDE=S△ADF=S△CEF=S△DEF
∴黑色大理石的面积与白色大理石面积的比是1：3．
故选C．
点评：本题构造的问题情境经常考查：根据三角形的中位线定理可以证明三角形被它的三条中位线分成的四个三角形全等．
练习册系列答案
相关题目
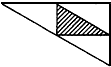厨房角柜的台面是三角形，如图，如果把各边中点的连线所围成的三角形铺成黑色大理石．（图中阴影部分）其余部分铺成白色大理石，那么黑色大理石的面积与白色大理石面积的比是（ ）
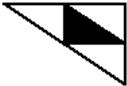17、厨房角柜的台面是三角形（如图所示），如果把各边中点连线所围成的三角形铺成黑色大理石（图中阴影部分），其余部分铺成白色大理石，则黑色大理石面积与白色大理石的面积之比是
