题目内容
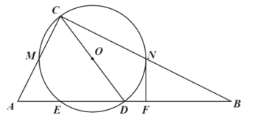
【题目】我们把“有两条边和其中一边的对角对应相等的两个三角形”叫做“同族三角形”,如图1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,则△ABC和△ABD是“同族三角形”.
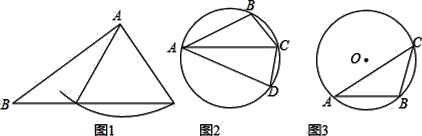
(1)如图2,四边形ABCD内接于圆,点C是弧BD的中点,求证:△ABC和△ACD是同族三角形;
(2)如图3,△ABC内接于⊙O,⊙O的半径为![]() ,AB=6,∠BAC=30°,求AC的长;
,AB=6,∠BAC=30°,求AC的长;
(3)如图3,在(2)的条件下,若点D在⊙O上,△ADC与△ABC是非全等的同族三角形,AD>CD,求![]() 的值.
的值.
【答案】(1)详见解析;(2)3![]() +3;(3)
+3;(3)![]() =
=![]() 或
或![]() .
.
【解析】
(1)由点C是弧BD的中点,根据弧与弦的关系,易得BC=CD,∠BAC=∠DAC,又由公共边AC,可证得:△ABC和△ACD是同族三角形;
(2)首先连接0A,OB,作点B作BE⊥AC于点E,易得△AOB是等腰直角三角形,继而求得答案;
(3)分别从当CD=CB时与当CD=AB时进行分析求解即可求得答案.
(1)证明:∵点C是弧BD的中点,即![]() ,
,
∴BC=CD,∠BAC=∠DAC,
∵AC=AC,
∴△ABC和△ACD是同族三角形.
(2)解:如图1,连接OA,OB,作点B作BE⊥AC于点E,
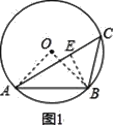
∵OA=OB=3![]() ,AB=6,
,AB=6,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,且∠AOB=90°,
∴∠C=∠AOB=45°,
∵∠BAC=30°,
∴BE=AB=3,
∴AE=![]() =3
=3![]() ,
,
∵CE=BE=3,
∴AC=AE+CE=3![]() +3.
+3.
(3)解:∵∠B=180°﹣∠BAC﹣∠ACB=180°﹣30°﹣45°=105°,
∴∠ADC=180°﹣∠B=75°,
如图2,当CD=CB时,∠DAC=∠BAC=30°,
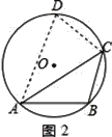
∴∠ACD=75°,
∴AD=AC=3![]() +3,CD=BC=
+3,CD=BC=![]() BE=3
BE=3![]() ,
,
∴![]() =
=![]() ;
;
如图3,当CD=AB时,过点D作DF⊥AC,交AC于点F,
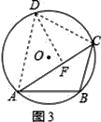
则∠DAC=∠ACB=45°,
∴∠ACD=180°﹣∠DAC﹣∠ADC=60°,
∴DF=CDsin60°=6×![]() =3
=3![]() ,
,
∴AD=![]() DF=
DF=![]() ,
,
∴![]() =
=![]() .
.
综上所述:![]() =
=![]() 或
或![]() .
.