题目内容
(本题满分9分)如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),
连接OD,过点D作DE⊥OD,交边AB于点E,连接OE。
(1)当CD=1时,求点E的坐标;
(2)如果设CD=t,梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这
个最大值及此时t的值;若不存在,请说明理由。
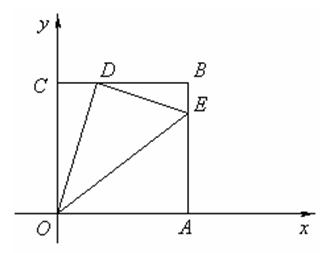
解:(1) 正方形OABC中,因为ED⊥OD,即∠ODE =90°
所以∠CDO+∠EDB=90°
即∠COD=90°-∠CDO 而 ∠EDB =90°-∠CDO
所以∠COD =∠EDB 又因为∠OCD=∠DBE=90°
所以△CDO∽△BED
所以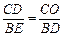 ,即
,即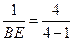 ,得BE=
,得BE=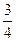
则: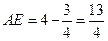 因此点E的坐标为(4,
因此点E的坐标为(4,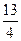 )。
)。
(2) 存在S的最大值。
由△CDO∽△BED∴ ,即
,即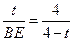 ,BE=t-
,BE=t-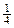 t2,
t2,
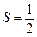 ×4×(4+t-
×4×(4+t-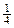 t2)
t2) 故当t=2时,S有最大值10。解析:
故当t=2时,S有最大值10。解析:
略
所以∠CDO+∠EDB=90°
即∠COD=90°-∠CDO 而 ∠EDB =90°-∠CDO
所以∠COD =∠EDB 又因为∠OCD=∠DBE=90°
所以△CDO∽△BED
所以
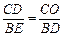 ,即
,即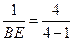 ,得BE=
,得BE=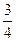
则:
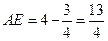 因此点E的坐标为(4,
因此点E的坐标为(4,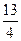 )。
)。(2) 存在S的最大值。
由△CDO∽△BED∴
 ,即
,即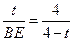 ,BE=t-
,BE=t-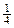 t2,
t2, 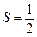 ×4×(4+t-
×4×(4+t-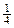 t2)
t2) 故当t=2时,S有最大值10。解析:
故当t=2时,S有最大值10。解析:略

练习册系列答案
相关题目
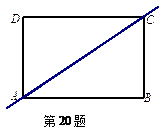
.(本题满分5分)如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
 |
1.若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为 cm.
2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?
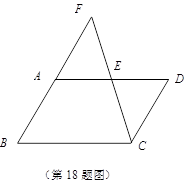
 交
交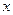 轴于
轴于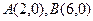 两点,交
两点,交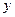 轴于点
轴于点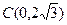 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线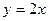 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交