题目内容
已知a、b、c、d为实数,且满足a+b+c+d+e=8,a2+b2+c2+d2+e2=16,试确定e的最大值.
答案:
解析:
解析:
|
解:由已知得a+b+c+d=8-e,a2+b2+c2+d2=16-e2 构造二次函数 y=4x2+2(a+b+c+d)x+(a2+b2+c2+d2), 则y=(x+a)2+(x+b)2+(x+c)2+(x+d)2≥0, ∴它的图像不在x轴下方,且开口向上, ∴△=4(a+b+c+d)2-16(a2+b2+c2+d2)≤0, ∴4(8-e)2-16(16-e2)≤0 化简,得5e2-16e≤0 解得0≤e≤ 所以e的最大值为 分析:不易直接求解.注意到已知条件中字母间的关系,把已知条件变形,恰当构造二次函数,利用一元二次方程的根的判别式巧妙解决. 说明:巧妙构造二次函数,使题目中的数量关系迅速明朗化,问题变得直观、简明了. |

练习册系列答案
相关题目
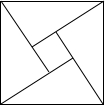 在赵爽弦图中,已知直角三角形的短直角边长为a,长直角边长为b,大正方形的面积为20,小正方形的面积为3,则(a+b)2的值是( )
在赵爽弦图中,已知直角三角形的短直角边长为a,长直角边长为b,大正方形的面积为20,小正方形的面积为3,则(a+b)2的值是( )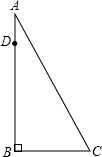 如图,AB为一棵大树,在树上距地面10米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为15米,求树高AB.
如图,AB为一棵大树,在树上距地面10米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为15米,求树高AB.