题目内容
阅读以下问题和解答过程：
如图1，在公路m旁有两工厂A、B，现要在公路上建一仓库．若要使仓库Q到A、B两工厂的距离之和最短，仓库应建在何处？
某同学正确地画出了图形，并写出了画图过程．
解：如图2，
①画点A关于公路m的对称点A1；
②画直线A1B与公路m交于一点Q，仓库应建在点Q的位置，此时仓库到A、B两工厂距离之和最短．
请你回答：这位同学断定仓库应建在“直线A1B与公路m的交点Q”的主要依据是：
如图1，在公路m旁有两工厂A、B，现要在公路上建一仓库．若要使仓库Q到A、B两工厂的距离之和最短，仓库应建在何处？
某同学正确地画出了图形，并写出了画图过程．
解：如图2，
①画点A关于公路m的对称点A1；
②画直线A1B与公路m交于一点Q，仓库应建在点Q的位置，此时仓库到A、B两工厂距离之和最短．
请你回答：这位同学断定仓库应建在“直线A1B与公路m的交点Q”的主要依据是：
三角形的任意两边之和大于第三边
三角形的任意两边之和大于第三边
．分析：在直线m上任意取一点D，连接AD，A1D，AQ，BD，根据轴对称的性质得出AD=A1D，AQ=A1Q，根据三角形的三边关系定理得出A1D+BD＞A1B，即可得出答案．
解答：解：在直线m上任意取一点D，连接AD，A1D，AQ，BD，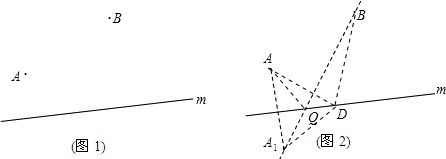
根据A关于直线m的对称点是A1，
∴AD=A1D，AQ=A1Q，
∴AQ+BQ=A1Q+BQ=BA1，
AD+BD=A1D+BD，
A1D+BD＞A1B，
∴AQ+BQ＜AD+BD，
即建在Q处最短（根据三角形的任意两边之和大于第三边）．
故答案为：三角形的任意两边之和大于第三边．
根据A关于直线m的对称点是A1，
∴AD=A1D，AQ=A1Q，
∴AQ+BQ=A1Q+BQ=BA1，
AD+BD=A1D+BD，
A1D+BD＞A1B，
∴AQ+BQ＜AD+BD，
即建在Q处最短（根据三角形的任意两边之和大于第三边）．
故答案为：三角形的任意两边之和大于第三边．
点评：本题主要考查对轴对称-最短路线问题，三角形的三边关系定理等知识点的理解和掌握，能根据作图得到的条件进行说理是解此题的关键．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
3、阅读理解：市盈率是某种股票每股市价与每股盈利的比率（即：某支股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利）．市盈率是估计股票价值的最基本、最重要的指标之一．一般认为该比率保持在30以下是正常的，风险小，值得购买；过大则说明股价高，风险大，购买时应谨慎．
阅读下列材料并解答。
例 平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
（1）分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
（2）归纳：考察点的个数和可连成直线的条数
发现：如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
(3)推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，
故应除以2；即
（4）
结论：
试探究以下几个问题：
平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
（1）分析：
当仅有3个点时，可作出 个三角形；
当仅有4个点时，可作出 个三角形；
当仅有5个点时，可作出 个三角形；
……
（2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）
| 点的 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n |
个数( 3 ) 推理：
（4）结论：
阅读理解：市盈率是某种股票每股市价与每股盈利的比率（即：某支股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利）．市盈率是估计股票价值的最基本、最重要的指标之一．一般认为该比率保持在30以下是正常的，风险小，值得购买；过大则说明股价高，风险大，购买时应谨慎．
应用：某日一股民通过互联网了解到如下三方面的信息：
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表：
③丙股票最近10天的市盈率依次为：
20 20 30 28 32 35 38 42 40 44
根据以上信息，解答下列问题：
（1）甲、乙两支股票的市盈率分别是多少？
（2）该股民所购买的15支股票中风险较小的有几支？
（3）求该股民所购15支股票的市盈率的平均数、中位数与众数；
（4）请根据丙股票最近10天的市盈率画出折线统计图，并依据市盈率的有关知识和折线统计图，就丙股票给该股民一个合理的建议．
应用：某日一股民通过互联网了解到如下三方面的信息：
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表：
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 市盈率 | 25 | 800 | 61 | 19 | 18 | 28 | 28 | 35 | 59 | 80 | 62 | 80 | 80 | 82 | 43 |
20 20 30 28 32 35 38 42 40 44
根据以上信息，解答下列问题：
（1）甲、乙两支股票的市盈率分别是多少？
（2）该股民所购买的15支股票中风险较小的有几支？
（3）求该股民所购15支股票的市盈率的平均数、中位数与众数；
（4）请根据丙股票最近10天的市盈率画出折线统计图，并依据市盈率的有关知识和折线统计图，就丙股票给该股民一个合理的建议．
（2007•常德）阅读理解：市盈率是某种股票每股市价与每股盈利的比率（即：某支股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利）．市盈率是估计股票价值的最基本、最重要的指标之一．一般认为该比率保持在30以下是正常的，风险小，值得购买；过大则说明股价高，风险大，购买时应谨慎．
应用：某日一股民通过互联网了解到如下三方面的信息：
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表：
③丙股票最近10天的市盈率依次为：
20 20 30 28 32 35 38 42 40 44
根据以上信息，解答下列问题：
（1）甲、乙两支股票的市盈率分别是多少？
（2）该股民所购买的15支股票中风险较小的有几支？
（3）求该股民所购15支股票的市盈率的平均数、中位数与众数；
（4）请根据丙股票最近10天的市盈率画出折线统计图，并依据市盈率的有关知识和折线统计图，就丙股票给该股民一个合理的建议．
应用：某日一股民通过互联网了解到如下三方面的信息：
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表：
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 市盈率 | 25 | 800 | 61 | 19 | 18 | 28 | 28 | 35 | 59 | 80 | 62 | 80 | 80 | 82 | 43 |
20 20 30 28 32 35 38 42 40 44
根据以上信息，解答下列问题：
（1）甲、乙两支股票的市盈率分别是多少？
（2）该股民所购买的15支股票中风险较小的有几支？
（3）求该股民所购15支股票的市盈率的平均数、中位数与众数；
（4）请根据丙股票最近10天的市盈率画出折线统计图，并依据市盈率的有关知识和折线统计图，就丙股票给该股民一个合理的建议．
（2007•常德）阅读理解：市盈率是某种股票每股市价与每股盈利的比率（即：某支股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利）．市盈率是估计股票价值的最基本、最重要的指标之一．一般认为该比率保持在30以下是正常的，风险小，值得购买；过大则说明股价高，风险大，购买时应谨慎．
应用：某日一股民通过互联网了解到如下三方面的信息：
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表：
③丙股票最近10天的市盈率依次为：
20 20 30 28 32 35 38 42 40 44
根据以上信息，解答下列问题：
（1）甲、乙两支股票的市盈率分别是多少？
（2）该股民所购买的15支股票中风险较小的有几支？
（3）求该股民所购15支股票的市盈率的平均数、中位数与众数；
（4）请根据丙股票最近10天的市盈率画出折线统计图，并依据市盈率的有关知识和折线统计图，就丙股票给该股民一个合理的建议．
应用：某日一股民通过互联网了解到如下三方面的信息：
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表：
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 市盈率 | 25 | 800 | 61 | 19 | 18 | 28 | 28 | 35 | 59 | 80 | 62 | 80 | 80 | 82 | 43 |
20 20 30 28 32 35 38 42 40 44
根据以上信息，解答下列问题：
（1）甲、乙两支股票的市盈率分别是多少？
（2）该股民所购买的15支股票中风险较小的有几支？
（3）求该股民所购15支股票的市盈率的平均数、中位数与众数；
（4）请根据丙股票最近10天的市盈率画出折线统计图，并依据市盈率的有关知识和折线统计图，就丙股票给该股民一个合理的建议．