题目内容
| |||||||||||
解析:
(1) |
由已知条件,得n2-1=0,解这个方程,得n1=1,n2=-1.当n=1时,得y=x2+x,此抛物线的顶点不在第四象限;当n=-1时,得y=x2-3x,此抛物线的顶点在第四象限.所以抛物线所对应的函数关系式为y=x2-3x. |
(2) |
解:由y=x2-3x,令y=0,得x2-3x=0,解得xl=0,x2=3,所以抛物线与x轴的另一个交点为(3,0),所以它的顶点为
①因为BC=1,由抛物线和矩形的对称性易知OB= ②因为点A在抛物线y=x2-3x上,故可设A点的坐标为(x,x2-3x),所以B点的坐标为(x,0)(0<x< 解题指导:(1)抛物线经过原点,则可将点(0,0)代人函数表达式;再根据顶点在第四象限则可确定函数的表达式. (2)将矩形ABCD的周长表示出来,再根据其特点求出最大值. |

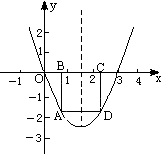
 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y= x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y= x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.