题目内容
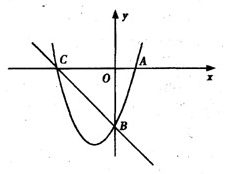
如图,已知抛物线y= x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y= x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
(1)填空:点C的坐标是 ,b= ,c= ;
(2)求线段QH的长(用含t的式子表示);
(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
(1)(0,-3),- ,-3;(2)|4-8t|;(3)t1=
,-3;(2)|4-8t|;(3)t1= -1,t2=
-1,t2=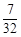 ,t3=
,t3=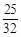
解析试题分析:(1)由于直线y= x-3过C点,因此C点的坐标为(0,-3),那么抛物线的解析式中c=-3,然后将A点的坐标代入抛物线的解析式中即可求出b的值;
x-3过C点,因此C点的坐标为(0,-3),那么抛物线的解析式中c=-3,然后将A点的坐标代入抛物线的解析式中即可求出b的值;
(2)求QH的长,需知道OQ,OH的长.根据CQ所在直线的解析式即可求出Q的坐标,也就得出了OQ的长,然后求OH的长.在(1)中可得出抛物线的解析式,那么可求出B的坐标.在直角三角形BPH中,可根据BP=5t以及∠CBO的正弦值(可在直角三角形COB中求出).得出BH的长,根据OB的长即可求出OH的长.然后OH,OQ的差的绝对值就是QH的长;
(3)本题要分①当H在Q、B之间.②在H在O,Q之间两种情况进行讨论;根据不同的对应角得出的不同的对应成比例线段来求出t的值.
(1)(0,-3),b=- ,c=-3.
,c=-3.
(2)由(1),得y= x2-
x2- x-3,它与x轴交于A,B两点,得B(4,0).
x-3,它与x轴交于A,B两点,得B(4,0).
∴OB=4,
又∵OC=3,
∴BC=5.
由题意,得△BHP∽△BOC,
∵OC∶OB∶BC=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,
∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由y=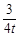 x-3与x轴交于点Q,得Q(4t,0).
x-3与x轴交于点Q,得Q(4t,0).
∴OQ=4t.
①当H在Q、B之间时,QH=OH-OQ=(4-4t)-4t=4-8t.
②当H在O、Q之间时,QH=OQ-OH=4t-(4-4t)=8t-4.
综合①,②得QH=|4-8t|;
(3)存在t的值,使以P、H、Q为顶点的三角形与△COQ相似.
①当H在Q、B之间时,QH=4-8t,
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得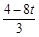 =
=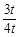 ,解得t=
,解得t=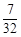
若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得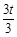 =
=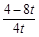 ,解得t1=
,解得t1= -1,t2=-
-1,t2=- -1(舍去).
-1(舍去).
②当H在O、Q之间时,QH=8t-4.
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得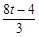 =
=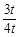 ,解得t=
,解得t=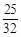 .
.
若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得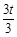 =
=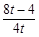 ,解得t1=t2=1(舍去).
,解得t1=t2=1(舍去).
综上所述,存在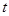 的值,t1=
的值,t1= -1,t2=
-1,t2=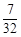 ,t3=
,t3=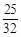 .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.