题目内容
【题目】如图,抛物线y=![]() x2+x﹣
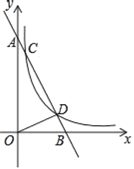
x2+x﹣![]() 与x轴相交于A,B两点,顶点为P.
与x轴相交于A,B两点,顶点为P.
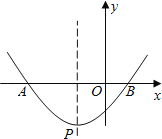
(1)求点A,点B的坐标;
(2)在抛物线上是否存在点E,使△ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由.
【答案】(1)A(﹣3,0),B(1,0);(2)存在符合条件的点E,其坐标为(﹣1﹣2![]() ,2)或(﹣1+2
,2)或(﹣1+2![]() ,2)或(﹣1,﹣2).
,2)或(﹣1,﹣2).
【解析】
(1)令y=0可求得相应方程的两根,则可求得A、B的坐标;
(2)可先求得P点坐标,则可求得点E到AB的距离,可求得E点纵坐标,再代入抛物线解析式可求得E点坐标.
(1)令y=0,则![]() x2+x
x2+x![]() 0,
0,
解得:x=﹣3或x=1,
∴A(﹣3,0),B(1,0);
(2)存在.理由如下:
∵y![]() x2+x
x2+x![]() (x+1)2﹣2,
(x+1)2﹣2,
∴P(﹣1,﹣2).
∵△ABP的面积等于△ABE的面积,
∴点E到AB的距离等于2,
①当点E在x轴下方时,则E与P重合,此时E(﹣1,﹣2);
②当点E在x轴上方时,则可设E(a,2),
∴![]() a2+a
a2+a![]() 2,解得:a=﹣1﹣2
2,解得:a=﹣1﹣2![]() 或a=﹣1+2
或a=﹣1+2![]() ,
,
∴E(﹣1﹣2![]() ,2)或E(﹣1+2
,2)或E(﹣1+2![]() ,2).
,2).
综上所述:存在符合条件的点E,其坐标为(﹣1﹣2![]() ,2)或(﹣1+2
,2)或(﹣1+2![]() ,2)或(﹣1,﹣2).
,2)或(﹣1,﹣2).

练习册系列答案
相关题目