题目内容
已知:抛物线y=ax2+bx+c经过点O(0,0),A(7,4),且对称轴l与x轴交于点B(5,0).(1)求抛物线的表达式;
(2)如图,点E、F分别是y轴、对称轴l上的点,且四边形EOBF是矩形,点C(5,
| 5 | 2 |
(3)在(2)的条件下,点G是对称轴l上的点,直线DG交CO于点H
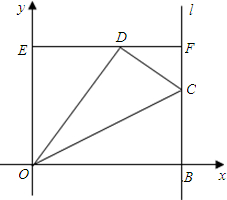 ,S△DOH:S△DHC=1:4,求G点坐标.
,S△DOH:S△DHC=1:4,求G点坐标.
分析:(1)利用待定系数法列方程组即可求出二次函数的系数,从而得到其解析式;
(2)根据翻折不变性,得到相等的线段和相等的角:BO=DO=5,CD=BC=
,∠OBC=∠ODC=90°,再根据互余关系,得到∠EOD=∠FDC,从而证出△EOD∽△FDC,再根据相似三角形的性质和矩形的性质列方程解答;
(3)过点H作HP⊥OB,根据等高的三角形面积比等于底的比,列出等式,求出OH与OC的比,从而得出D、H坐标,解出直线DG的表达,进而求出G点坐标.
(2)根据翻折不变性,得到相等的线段和相等的角:BO=DO=5,CD=BC=
| 5 |
| 2 |
(3)过点H作HP⊥OB,根据等高的三角形面积比等于底的比,列出等式,求出OH与OC的比,从而得出D、H坐标,解出直线DG的表达,进而求出G点坐标.
解答:解:(1)由题意得
(1分),
解得
,
∴y=-
x2+
x.(3分)
(2)∵△BOC与△DOC重合,OB=5,BC=
,
∴BO=DO=5,CD=BC=
,∠OBC=∠ODC=90°,
∴∠EDO+∠FDC=90°,又∠EDO+∠EOD=90°,
∴∠EOD=∠FDC,
∵∠OED=∠DFC=90°,
∴△EOD∽△FDC,(2分)
∴
=
=
=
=2,(1分)
∵四边形OEFB是矩形,
∴EF=OB,EO=FB,
设FC=x,则ED=2x,DF=5-2x,
∴EO=10-4x,
∴10-4x=
+x,解,得x=
,
∴ED=3,EO=4,
∴D(3,4).(1分)
(3)过点H作HP⊥OB,垂足为点P.
∵S△DOH:S△DHC=1:4,
∴
=
=
,(1分)
∵HP⊥OB,CB⊥OB,
∴HP∥BC,
∴
=
=
=
,
∴OP=1,PH=
,
∴H(1,
),(1分)
∴经过点D(3,4),H(1,
)的直线DG的表达式为y=
x-
,(1分)
∴G(5,
).(1分)
|
解得
|
∴y=-
| 4 |
| 21 |
| 40 |
| 21 |
(2)∵△BOC与△DOC重合,OB=5,BC=
| 5 |
| 2 |
∴BO=DO=5,CD=BC=
| 5 |
| 2 |
∴∠EDO+∠FDC=90°,又∠EDO+∠EOD=90°,
∴∠EOD=∠FDC,
∵∠OED=∠DFC=90°,
∴△EOD∽△FDC,(2分)
∴
| ED |
| FC |
| EO |
| DF |
| OD |
| CD |
| 5 | ||
|
∵四边形OEFB是矩形,
∴EF=OB,EO=FB,
设FC=x,则ED=2x,DF=5-2x,
∴EO=10-4x,
∴10-4x=
| 5 |
| 2 |
| 3 |
| 2 |
∴ED=3,EO=4,
∴D(3,4).(1分)
(3)过点H作HP⊥OB,垂足为点P.
∵S△DOH:S△DHC=1:4,
∴
| S△DOH |
| S△DHC |
| OH |
| HC |
| 1 |
| 4 |
∵HP⊥OB,CB⊥OB,
∴HP∥BC,
∴
| OH |
| OC |
| OP |
| OB |
| PH |
| BC |
| 1 |
| 5 |
∴OP=1,PH=
| 1 |
| 2 |
∴H(1,
| 1 |
| 2 |
∴经过点D(3,4),H(1,
| 1 |
| 2 |
| 7 |
| 4 |
| 5 |
| 4 |
∴G(5,
| 15 |
| 2 |
点评:本题主要考查了二次函数解析式的确定、翻折变换及三角形的面积等知识.主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
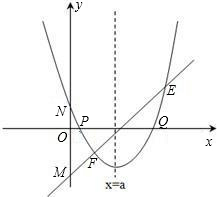 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.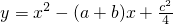 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.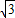 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.