题目内容
【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 ![]() (元)与销售单价
(元)与销售单价 ![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
【答案】
(1)解:由题意得,销售量= ![]() ,
,
则 ![]() ;
;
(2)解:方案A:由题可得 ![]() ,因为
,因为 ![]() ,对称轴为x=35,
,对称轴为x=35,
抛物线开口向下,在对称轴左侧, ![]() 随
随 ![]() 的增大而增大,
的增大而增大,
所以,当x=30时,w取最大值为2000元,
方案B:由题意得 ![]()
解得: ![]() ,
,
在对称轴右侧,w随x的增大而减小,
所以,当x=45时,w取最大值为1250元
因为2000元>1250元,
所以选择方案A.
【解析】(1)先求出上涨后的销售量,再根据利润=(销售单价-进价)×销售量,列出函数关系式即可。
(2)根据(1)式列出的函数关系式,运用配方法求最大值。
(3)分别求出方案A、B中x的取值范围,再根据二次函数的性质分别求出A、B方案的最大利润,然后进行比较。

【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |
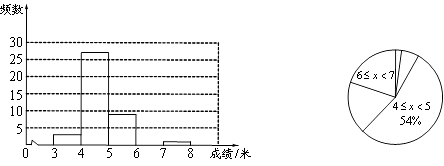
请你结合图表中所提供的信息,回答下列问题:
(1)表中m= , n=;
(2)请补全频数分布直方图;
(3)在扇形统计图中, ![]() 这一组所占圆心角的度数为度;
这一组所占圆心角的度数为度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.