题目内容
在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是
.
(1)求暗箱中红球的个数.
(2)小军和小明做游戏,游戏规则是:先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,若两次摸到的球颜色不同,则小军胜,否则小明胜.你认为这个游戏公平吗?(用树形图或列表法求解).
| 1 | 4 |
(1)求暗箱中红球的个数.
(2)小军和小明做游戏,游戏规则是:先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,若两次摸到的球颜色不同,则小军胜,否则小明胜.你认为这个游戏公平吗?(用树形图或列表法求解).
分析:(1)设红球个数为x个,根据题意列出方程,求出方程的解即可得到红球的个数;
(2)列表得出所有等可能的情况数,找出两次摸到的球颜色不同的情况,求出小军获胜额概率,以及小明获胜的概率,即可做出判断.
(2)列表得出所有等可能的情况数,找出两次摸到的球颜色不同的情况,求出小军获胜额概率,以及小明获胜的概率,即可做出判断.
解答:解:(1)设暗箱中红球的个数为x个,
根据题意得:
=
,即x=2,
则暗箱中红球的个数为2个;
(2)列表如下:
所有等可能的情况有16种,其中两次摸到的球颜色不同的情况有10种,相同的有6种,
则P(小军获胜)=
=
,P(小明获胜)=
=
,
∵
>
,
∴该游戏不公平.
根据题意得:
| 1 |
| 2+x |
| 1 |
| 4 |
则暗箱中红球的个数为2个;
(2)列表如下:
| 红 | 红 | 黄 | 白 | |
| 红 | (红,红) | (红,红) | (黄,红) | (白,红) |
| 红 | (红,红) | (红,红) | (黄,红) | (白,红) |
| 黄 | (红,黄) | (红,黄) | (黄,黄) | (白,黄) |
| 白 | (红,白) | (红,白) | (黄,白) | (白,白) |
则P(小军获胜)=
| 10 |
| 16 |
| 5 |
| 8 |
| 6 |
| 16 |
| 3 |
| 8 |
∵
| 5 |
| 8 |
| 3 |
| 8 |
∴该游戏不公平.
点评:此题考查了游戏的公平性,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
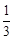 .
. .
.