题目内容
在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是![]() .
.
(1)求暗箱中红球的个数.
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
考点:
列表法与树状图法;概率公式.
专题:
图表型.
分析:
(1)设红球有x个,根据概率的意义列式计算即可得解;
(2)画出树状图,然后根据概率公式列式计算即可得解.
解答:
解:(1)设红球有x个,
根据题意得,![]() =
=![]() ,
,
解得x=1;
(2)根据题意画出树状图如下:
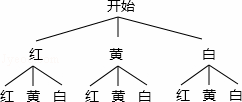
一共有9种情况,两次摸到的球颜色不同的有6种情况,
所以,P(两次摸到的球颜色不同)=![]() =
=![]() .
.
点评:
本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 .
. .
.