题目内容
【题目】
如图
，在正方形
中，点
、
、
分别在
、
、
上，且
，垂足为
，那么
与
________（“相等”或“不相等”）26.
如图
，将边长为
的正方形纸片沿折叠，使得点
落到边上．若
，求出
和的长度．
【答案】（1）相等；（2）
【解析】
（1）可过点E作EH∥AD，证明Rt△ABG≌Rt△EHF即可得出结论．
（2）借助对称原理，根据勾股定理即可求出BE、AG的长；利用第（1）问中的结论即可获得EF的长．
（1）如图（1）所示，
过点E作EH∥AD，交CD于H；则四边形AEHD为矩形；
∴EH=AD=AB；
∵AG⊥EF，EH∥AD，
∴∠BAG+∠AEF=90°，∠AEF+∠FEH=90°，
∴∠BAG=∠FEH；在△ABG与△EHF中，
∵
，
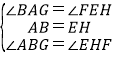∴△ABG≌△EHF（ASA）
∴AG=EF．
故答案为相等；
如图，连接
；
设
，则
；由对称原理得：
，
，
∴
；由问题
知：
；
∵四边形
为正方形，
∴
；
由勾股定理得：
，
；
，解得
，
∴
，．
练习册系列答案
相关题目
