题目内容
【题目】已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
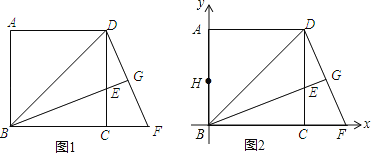
(1)求证:△BCE≌△DCF;
(2)求CF的长;
(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.
【答案】(1)见解析;(2)![]() ﹣1;(3)所有符合条件的P点坐标为(2﹣
﹣1;(3)所有符合条件的P点坐标为(2﹣![]() ,2﹣
,2﹣![]() )、(﹣2+
)、(﹣2+![]() ,﹣2+
,﹣2+![]() )、(
)、(![]() ﹣1,
﹣1,![]() ﹣1)、(
﹣1)、(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用正方形的性质,由全等三角形的判定定理SAS即可证得△BCE≌△DCF;
(2)通过△DBG≌△FBG的对应边相等知BD=BF=![]() ;然后由CF=BF﹣BC=即可求得;
;然后由CF=BF﹣BC=即可求得;
(3)分三种情况分别讨论即可求得.
【解答】(1)证明:如图1,
在△BCE和△DCF中,
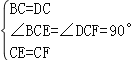 ,
,
∴△BCE≌△DCF(SAS);
(2)证明:如图1,
∵BE平分∠DBC,OD是正方形ABCD的对角线,
∴∠EBC=![]() ∠DBC=22.5°,
∠DBC=22.5°,
由(1)知△BCE≌△DCF,
∴∠EBC=∠FDC=22.5°(全等三角形的对应角相等);
∴∠BGD=90°(三角形内角和定理),
∴∠BGF=90°;
在△DBG和△FBG中,
 ,
,
∴△DBG≌△FBG(ASA),
∴BD=BF,DG=FG(全等三角形的对应边相等),
∵BD=![]() =
=![]() ,
,
∴BF=![]() ,
,
∴CF=BF﹣BC=![]() ﹣1;
﹣1;
(3)解:如图2,∵CF=![]() ﹣1,BH=CF
﹣1,BH=CF
∴BH=![]() ﹣1,
﹣1,
①当BH=BP时,则BP=![]() ﹣1,
﹣1,
∵∠PBC=45°,
设P(x,x),
∴2x2=(![]() ﹣1)2,
﹣1)2,
解得x=2﹣![]() 或﹣2+
或﹣2+![]() ,
,
∴P(2﹣![]() ,2﹣
,2﹣![]() )或(﹣2+
)或(﹣2+![]() ,﹣2+
,﹣2+![]() );
);
②当BH=HP时,则HP=PB=![]() ﹣1,
﹣1,
∵∠ABD=45°,
∴△PBH是等腰直角三角形,
∴P(![]() ﹣1,
﹣1,![]() ﹣1);
﹣1);
③当PH=PB时,∵∠ABD=45°,
∴△PBH是等腰直角三角形,
∴P(![]() ,
,![]() ),
),
综上,在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形,所有符合条件的P点坐标为(2﹣![]() ,2﹣
,2﹣![]() )、(﹣2+
)、(﹣2+![]() ,﹣2+
,﹣2+![]() )、(
)、(![]() ﹣1,
﹣1,![]() ﹣1)、(
﹣1)、(![]() ,
,![]() ).
).