题目内容
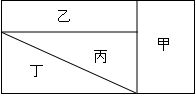 如图所示的长方形中,甲、乙、丙、丁四块面积相等,甲的长是宽的2倍,设乙的长和宽分别是a和b,则a:b=
如图所示的长方形中,甲、乙、丙、丁四块面积相等,甲的长是宽的2倍,设乙的长和宽分别是a和b,则a:b=分析:本题中面积相等是等量关系,可用列方程求边长的关系.设甲的宽是x,长为2x,面积为2x2,乙,丙的面积相等,可以求出乙的宽和丙的短直角边的关系,把a和b都用x表示出来,然后求出比.
解答:解:设甲的宽为x,长为2x.
乙的面积为:ab=2x2(1)
设丙的短直角边为c:
ac=2x2(2)
(1)和(2)联立可求出c=2b
∵c+b=2x
∴b=
x(3)
把(3)代入(1)式得a=3x
a:b=9:2
故答案为9:2.
乙的面积为:ab=2x2(1)
设丙的短直角边为c:
| 1 |
| 2 |
(1)和(2)联立可求出c=2b
∵c+b=2x
∴b=
| 2 |
| 3 |
把(3)代入(1)式得a=3x
a:b=9:2
故答案为9:2.
点评:本题考查的是数形结合的思想,通过所给的面积相等以及甲的宽和长的关系求出a和b的关系.

练习册系列答案
相关题目

 .
. 
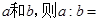 .
. 
