题目内容
【题目】如图,在3×3的正方形网格中标出了∠1和∠2。则∠1+∠2=。 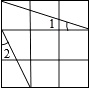
【答案】45°
【解析】解 :连接AC,BC .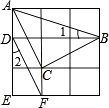
根据勾股定理,AC=BC=![]() ;AB=
;AB=![]()
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2 ,
)2 ,
∴△ABC是等腰直角三角形,
∴∠ACB=90,∠CAB=45.
∵AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠2=∠DAC;
在Rt△ABD中,
∠1+∠DAB=90;
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90 ,
∴∠1+∠DAC=45 ,
∴∠1+∠2=∠1+∠DAC=45.
故答案为:45.
连接AC,BC ;利用方格纸的特点,根据勾股定理得出AC,BC,AB的长, 然后根据勾股定理的逆定理判断出 △ABC是等腰直角三角形,从而得出 ∠ACB=90,∠CAB=45.根据一组对边平行且相等的四边形是平行四边形得出 四边形ADFC是平行四边形,根据平行四边形的对边平行得出AC∥DF,根据二直线平行同位角相等得出∠2=∠DAC;根据直角三角形两锐角互余得出∠1+∠DAB=90;,根据角的和差及等量代换得出∠1+∠2=∠1+∠DAC=45.

练习册系列答案
相关题目