题目内容
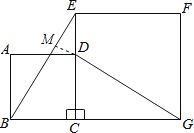
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG . 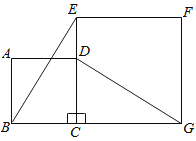
(1)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.
(2)观察猜想BE与DG之间的关系,并证明你的结论.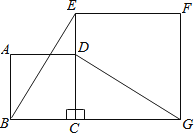
【答案】
(1)
【解答】存在.
∵四边形ABCD和CEFG为正方形,
∴CB=CD,CE=CG,∠BCD=∠ECG=90°,
∴把△CBE绕点C顺时针旋转90°可得△CDG;
(2)
【解答】BE=DG,BE⊥DG.理由如下:
延长GD交BE于M,如图,
∵△CBE绕点C顺时针旋转90°可得△CDBG,
∴BE=DG,∠BEC=∠DGC,
∵∠BEC+∠CBE=90°,
∴∠BEC+∠DGC=90°,
∴∠BMG=90°,
∴DG⊥BE.
【解析】(1)根据正方形的性质得CB=CD , CE=CG , ∠BCD=∠ECG=90°,则可根据旋转的定义,把△CBE绕点C顺时针旋转90°可得△CDG;(2)根据旋转的性质得BE=DG , ∠BEC=∠DGC , 由于∠BEC+∠CBE=90°,则∠BEC+∠DGC=90°,于是可判断DG⊥BE .
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
相关题目
【题目】某种油菜籽在相同条件下发芽试验的结果如下:
每批粒数 | 100 | 400 | 800 | 1000 | 2000 | 4000 |
发芽的频数 | 85 | 300 | 652 | 793 | 1604 | 3204 |
发芽的频率 | 0.850 | 0.750 | 0.815 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计该油菜种子发芽的概率为_______(精确到0.1).