题目内容
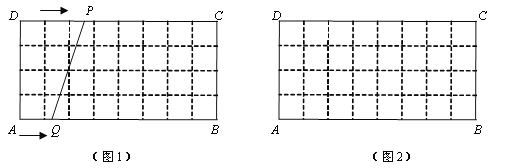
【题目】如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).
(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ并求其长度;
(2)当t为多少时,△PQB是以BP为底的等腰三角形.
【答案】(1)5;(2)6.
【解析】
试题分析:(1)根据点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位可知,当t=6秒时,DP=6,AQ=3即可画出线段PQ;
(2)设时间为t,则在t秒钟,P运动了2t个单位,Q运动了t个单位,由题意得 PQ=BQ,然后根据勾股定理列出关于t的方程,解得t即可.
试题解析:(1)∵点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当运动时间t为6秒,
∴由图中可知PQ的位置如下图2,
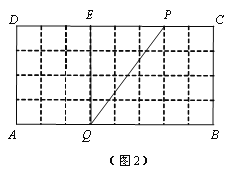
则由已知条件可得PD=6,AQ=3,QE=4,PE=3,
∴PQ=5.
(2)能.由题意得 PQ=BQ ,(t﹣![]() t)2+42=(8﹣
t)2+42=(8﹣![]() t)2
t)2
解得t=6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

