题目内容
4、若一个等腰三角形的底角是15°，腰长为2cm，则这个腰三角形腰上的高的长度为
1cm
．分析：根据等腰三角形的性质可求得两底角的度数，从而可求得顶角的邻补角的度数为30°，根据直角三角形中30度的角所对的边是斜边的一半即可求得腰上的高的长．
解答：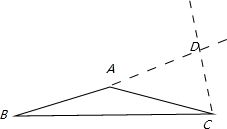
解：如图∠B=15°，AB=AC，CD为腰AB上的高，AC=2cm，
∠B=15°，AB=AC，
∴∠DAC=30°，
∵CD为AB上的高，AC=2cm，
∴CD=1cm．
故答案为：1cm．
解：如图∠B=15°，AB=AC，CD为腰AB上的高，AC=2cm，∠B=15°，AB=AC，
∴∠DAC=30°，
∵CD为AB上的高，AC=2cm，
∴CD=1cm．
故答案为：1cm．
点评：此题主要考查等腰三角形的性质及含30度的直角三角形的性质的综合运用能力．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
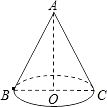如图，圆锥的轴截面△ABC是一个以圆锥的底面直径为底边，圆锥的母线为腰的等腰三角形，若圆锥的底面直径BC=4cm，母线AB=6cm，则由点B出发，经过圆锥的侧面到达母线AC的最短路程是（ ）A、
| ||||
| B、6cm | ||||
C、3
| ||||
| D、4cm |
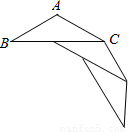
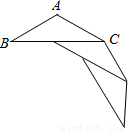
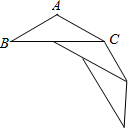（2012•江西模拟）在等腰三角形ABC中，AB=AC，∠B=30°，若将若干个这样的三角形按如图所示的方式拼接在一起，使每个等腰三角形的顶角的顶点与前一个三角形的底角顶点重合，一腰在前一个等腰三角形的底边上，直至最后一个三角形的底角顶点与点A重合，则这样拼成的多边形的形状为
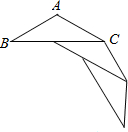在等腰三角形ABC中，AB=AC，∠B=30°，若将若干个这样的三角形按如图所示的方式拼接在一起，使每个等腰三角形的顶角的顶点与前一个三角形的底角顶点重合，一腰在前一个等腰三角形的底边上，直至最后一个三角形的底角顶点与点A重合，则这样拼成的多边形的形状为________．
