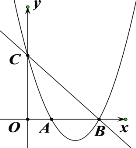
题目内容
【题目】问题1如图①点A、B、C在⊙O上，且∠ABC=120°，⊙O的半径是3.求弧AC的长.
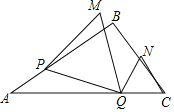
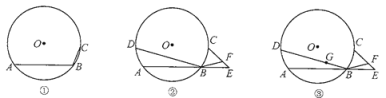
问题2如图②点A、B、C、D在⊙
上，且弧AD=弧BC，E是AB的延长线上的
.
(1)设BD=nBF，则n=________;
(2)如图③若G是线段BD上的一个点，且
.试探究，在⊙上是否存在点P (B除外)使PG=PF?为什么?
【答案】问题1：
；问题2：(1)
；(1)详见解析
【解析】
问题一：根据弧长的计算公式，根据∠ABC=120°，找到∠AOC的度数，再由弧长公式计算出弧AC的长即可；
问题二：(1)连接AC，易证AC=3BF，然后再证明AC=BD，可得到n的值；
(2) 由（1）可证BG=BF，过点B作AE的垂线，与圆的交点即是点P.
问题一：解：如图，连接OA和OC
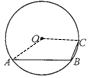
∵∠ABC=120°
∴∠AOC=360°-2∠ABC=120°
∴
=
=
问题2：解：(1)如图，连接AC
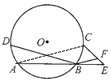
∵弧AD=弧BC
∴弧BD=弧AC
∴BD=AC
∵
∴
，∠BEF=∠AEC
∴△BEF∽△AEC
∴
∴
，即3BF=BD
∴n=3
(2) 如图，连接GF,过点B作AE的垂线，与GF交于点H，与圆的交点即是点P
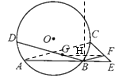
由(1)得△BEF∽△AEC，
∵
∴BF=BG
∴△BGF为等腰三角形
∴∠FBE=∠CAE
∵弧AD=弧BC
∴∠ABD=∠CAB
∴∠DBA=∠FBE
∵∠ABH=∠EBH=90°
∴∠DBH=∠FBH
∴BH为GF的中垂线
∴PG=PF
故存在P.
练习册系列答案
相关题目
