��Ŀ����
��ͼ����֪������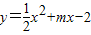 ��ֱ��y=x����A��B���㣬��y�ύ�ڵ�C����BC��x�ᣮ
��ֱ��y=x����A��B���㣬��y�ύ�ڵ�C����BC��x�ᣮ��1���������ߵĽ���ʽ��
��2����D��E���߶�AB������A��B���������㣨��E�ڵ�D���Ϸ�����DE=
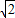 ����D��E����ֱ���y���ƽ���ߣ�����������F��G������D��ĺ�����Ϊx���ı���DEGF�����Ϊy����y��x֮��Ĺ�ϵʽ����д���Ա���x��ȡֵ��Χ��
����D��E����ֱ���y���ƽ���ߣ�����������F��G������D��ĺ�����Ϊx���ı���DEGF�����Ϊy����y��x֮��Ĺ�ϵʽ����д���Ա���x��ȡֵ��Χ����3������2���е��߶�DE���ƶ������У��ı���DEGF�ܷ��Ϊ���Σ����ܣ��������Ӧx��ֵ�������ܣ���˵�����ɣ�
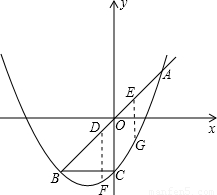
���𰸡���������1���������ߵĽ���ʽ֪����C��������Ϊ-2����BC��x�ᣬ��ô��B��������ҲΪ-2������ֱ��AB�Ľ���ʽ����ȷ��B������꣬Ȼ������������ߵĽ���ʽ�У������m��ֵ���Ӷ�ȷ���������ߵĽ���ʽ��
��2����D��DM��EG��M����֪��EDM=45°����ôDM=1���������D�ĺ����꣬��������DM�ij���ʾ��E��ĺ����꣬��ֱ��AB�������ߵĽ���ʽ�����D��E��F��G�������꣬�Ӷ��õ�DF��EC�ij��������ı���ECFD�Ǹ����Σ���ô�������ε������ʽ���ɵõ�y��x�ĺ�����ϵʽ��
��3�����ı���EGFD�����Σ�����Ӧ�������ı���EGFD�Ǹ�ƽ���ı��Σ���ôEG=DF���ɸ��ݣ�2����õ��������߶εı���ʽ���з��������DF��CE�ij���Ȼ���ж�DF�Ƿ���DE��ȼ��ɣ�
����⣺��1����֪C��0��-2������B���������ҲΪ-2��
���ڵ�B��ֱ��y=x�ϣ���B��-2��-2�������������ߵĽ���ʽ�У��ɵã�
 ��-2��2-2m-2=-2��
��-2��2-2m-2=-2��
���m=1��
�ʣ�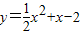 ��
��
��2����D��DM��EG��M��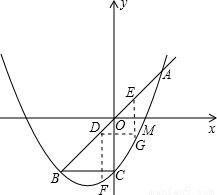
��DEM�У�DE=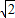 ����EDM=45°����DM=1��
����EDM=45°����DM=1��
��D��x��x������E��x+1��x+1����
F��x�� x2+x-2����G��x+1��
x2+x-2����G��x+1�� ��x+1��2+��x+1��-2����
��x+1��2+��x+1��-2����
��DF=x-�� x2+x-2��=2-
x2+x-2��=2- x2��
x2��
EG=��x+1��-[ ��x+1��2+��x+1��-2]=2-
��x+1��2+��x+1��-2]=2- ��x+1��2��
��x+1��2��
��y= ��DF+EG��×DM=
��DF+EG��×DM= [2-
[2- x2+2-
x2+2- ��x+1��2]×1��
��x+1��2]×1��
�����ã�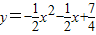 ��
��
x��ȡֵ��Χ��-2��x��1��
��3���ı���DEGF���ܳ�Ϊ���Σ��������£�
���ı���DEGF�����Σ����ı���DEGF�����Ǹ�ƽ���ı��Σ��ã�
DF=EG��
��2- x2=2-
x2=2- ��x+1��2��
��x+1��2��
���x=- ��
��
��DF=EG=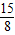 ��DE��
��DE��
���ı���DEGF�����ܳ�Ϊ���Σ�
���������⿼���˶��κ�������ʽ��ȷ����ͼ������������ε��ж�������֪ʶ���Ѷ����У�
��2����D��DM��EG��M����֪��EDM=45°����ôDM=1���������D�ĺ����꣬��������DM�ij���ʾ��E��ĺ����꣬��ֱ��AB�������ߵĽ���ʽ�����D��E��F��G�������꣬�Ӷ��õ�DF��EC�ij��������ı���ECFD�Ǹ����Σ���ô�������ε������ʽ���ɵõ�y��x�ĺ�����ϵʽ��
��3�����ı���EGFD�����Σ�����Ӧ�������ı���EGFD�Ǹ�ƽ���ı��Σ���ôEG=DF���ɸ��ݣ�2����õ��������߶εı���ʽ���з��������DF��CE�ij���Ȼ���ж�DF�Ƿ���DE��ȼ��ɣ�
����⣺��1����֪C��0��-2������B���������ҲΪ-2��
���ڵ�B��ֱ��y=x�ϣ���B��-2��-2�������������ߵĽ���ʽ�У��ɵã�
 ��-2��2-2m-2=-2��
��-2��2-2m-2=-2�����m=1��
�ʣ�
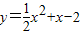 ��
����2����D��DM��EG��M��

��DEM��DE=
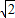 ����EDM=45°����DM=1��
����EDM=45°����DM=1����D��x��x������E��x+1��x+1����
F��x��
 x2+x-2����G��x+1��
x2+x-2����G��x+1�� ��x+1��2+��x+1��-2����
��x+1��2+��x+1��-2������DF=x-��
 x2+x-2��=2-
x2+x-2��=2- x2��
x2��EG=��x+1��-[
 ��x+1��2+��x+1��-2]=2-
��x+1��2+��x+1��-2]=2- ��x+1��2��
��x+1��2����y=
 ��DF+EG��×DM=
��DF+EG��×DM= [2-
[2- x2+2-
x2+2- ��x+1��2]×1��
��x+1��2]×1�������ã�
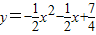 ��
��x��ȡֵ��Χ��-2��x��1��
��3���ı���DEGF���ܳ�Ϊ���Σ��������£�
���ı���DEGF�����Σ����ı���DEGF�����Ǹ�ƽ���ı��Σ��ã�
DF=EG��
��2-
 x2=2-
x2=2- ��x+1��2��
��x+1��2�����x=-
 ��
����DF=EG=
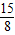 ��DE��
��DE�����ı���DEGF�����ܳ�Ϊ���Σ�
���������⿼���˶��κ�������ʽ��ȷ����ͼ������������ε��ж�������֪ʶ���Ѷ����У�

��ϰ��ϵ�д�
�����Ŀ
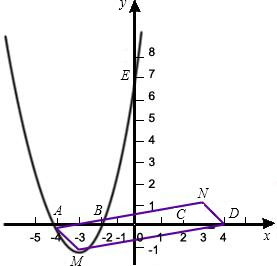 ��ͼ����֪������C1��������Ľ���������A��-4��0����B��-2��0����E��0��8����
��ͼ����֪������C1��������Ľ���������A��-4��0����B��-2��0����E��0��8����
 ��������Ľ���������A(��4��0)��B(��2��0)��E(0��8)��
��������Ľ���������A(��4��0)��B(��2��0)��E(0��8)��
 ����ԭ��ԳƵ�������
����ԭ��ԳƵ������� �Ľ���ʽ��
�Ľ���ʽ�� ��x��ֱ���C��D����(��C�ڵ�D�����)������ΪN���ı���MDNA�����ΪS������A����Dͬʱ��ÿ��1����λ���ٶ���ˮƽ����ֱ����ҡ������˶������ͬʱ����M����Nͬʱ��ÿ��2����λ���ٶ�����ֱ����ֱ����¡������˶���ֱ����A���D�غ�Ϊֹ������ı���MDNA�����S���˶�ʱ��t֮��Ĺ�ϵʽ����д���Ա���t��ȡֵ��Χ��
��x��ֱ���C��D����(��C�ڵ�D�����)������ΪN���ı���MDNA�����ΪS������A����Dͬʱ��ÿ��1����λ���ٶ���ˮƽ����ֱ����ҡ������˶������ͬʱ����M����Nͬʱ��ÿ��2����λ���ٶ�����ֱ����ֱ����¡������˶���ֱ����A���D�غ�Ϊֹ������ı���MDNA�����S���˶�ʱ��t֮��Ĺ�ϵʽ����д���Ա���t��ȡֵ��Χ��
