题目内容
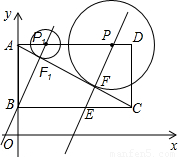
(2004•南通)已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1.(1)求BC、AP1的长;
(2)设AP=m,梯形PECD的面积为S,求S与m之间的函数关系式,写出自变量m的取值范围;
(3)以点E为圆心作⊙E与x轴相切.
①探究并猜想:⊙P和⊙E有哪几种位置关系,并求出AP相应的取值范围;
②当直线L把矩形ABCD分成两部分的面积之比值为3:5时,则⊙P和⊙E的位置关系如何并说明理由.
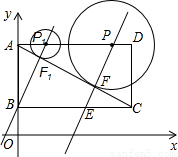
【答案】分析:(1)求BC、AP1的长,因为BC=2AB,可以根据直线的解析式是y=2x+1,确定B、P1的坐标,得出AB的距离,从而求出;
(2)根据梯形PECD的面积公式求出PD、EC、CD的长,从而求出S与m之间的函数关系式,及自变量m的取值范围;
(3)根据圆与圆的位置关系,圆心距>两圆的半径时外离,圆心距=两圆的半径时相切,圆心距<两圆的半径时相交,求出AP相应的取值范围,确定⊙P和⊙E的位置关系.
解答:解:(1)BC=4,AP1=1.y=2x+1,可以求出B(0,1),P1(1,3),AB=3-1=2,BC=2AB=4,AP1=1;
(2)S=9-2m;
∵1≤m<4,
∴PD=4-m,EC=4-m+1=5-m,CD=2,
∴S=0.5(4-m+5-m)×2=9-2m(1≤m<4);
(3)①在RT△ABP1中,
∵AB=2,AP1=1,
∴BP1=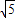 ,点P在AD上运动时,PF=PE-EF=
,点P在AD上运动时,PF=PE-EF= -1,
-1,
当⊙P和⊙E相切时,PF=PE-EF= -1;
-1;
∵RT△APF∽RT△ACD,
∴AP:AC=PF:CD,
∴AP=5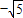 ,
,
∴当1≤m<5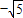 时,两圆外离,
时,两圆外离,
当m=5 时,两圆外切,
时,两圆外切,
当5 <m<4时,两圆相交.
<m<4时,两圆相交.
②外离或相交.理由如下:
∵矩形ABCD的面积是8,且直线L把矩形ABCD分成两部分的面积之比值为3:5,
∴S四边形PECD=5或者S四边形PECD=3,
当S四边形PECD=5时,9-2m=5,m=2,即AP=2,
∴1≤AP<5 ,
,
∴此时两圆外离.
当S四边形PECD=3时,9-2m=3,m=3,即AP=3,
∴5 <AP<4,
<AP<4,
∴此时两圆相交.
点评:本题综合考查了函数解析式,及直线与圆、圆与圆的位置关系.圆与圆的位置关系有:相离(外离,内含),相交、相切(外切、内切),直线和圆的位置关系有:相交、相切、相离,所以这样一来,我们在分析过程中不能忽略所有的可能情况.
(2)根据梯形PECD的面积公式求出PD、EC、CD的长,从而求出S与m之间的函数关系式,及自变量m的取值范围;
(3)根据圆与圆的位置关系,圆心距>两圆的半径时外离,圆心距=两圆的半径时相切,圆心距<两圆的半径时相交,求出AP相应的取值范围,确定⊙P和⊙E的位置关系.
解答:解:(1)BC=4,AP1=1.y=2x+1,可以求出B(0,1),P1(1,3),AB=3-1=2,BC=2AB=4,AP1=1;
(2)S=9-2m;
∵1≤m<4,
∴PD=4-m,EC=4-m+1=5-m,CD=2,
∴S=0.5(4-m+5-m)×2=9-2m(1≤m<4);
(3)①在RT△ABP1中,
∵AB=2,AP1=1,
∴BP1=
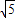 ,点P在AD上运动时,PF=PE-EF=
,点P在AD上运动时,PF=PE-EF= -1,
-1,当⊙P和⊙E相切时,PF=PE-EF=
 -1;
-1;∵RT△APF∽RT△ACD,
∴AP:AC=PF:CD,
∴AP=5
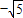 ,
,∴当1≤m<5
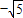 时,两圆外离,
时,两圆外离,当m=5
 时,两圆外切,
时,两圆外切,当5
 <m<4时,两圆相交.
<m<4时,两圆相交.②外离或相交.理由如下:
∵矩形ABCD的面积是8,且直线L把矩形ABCD分成两部分的面积之比值为3:5,
∴S四边形PECD=5或者S四边形PECD=3,
当S四边形PECD=5时,9-2m=5,m=2,即AP=2,
∴1≤AP<5
 ,
,∴此时两圆外离.
当S四边形PECD=3时,9-2m=3,m=3,即AP=3,
∴5
 <AP<4,
<AP<4,∴此时两圆相交.
点评:本题综合考查了函数解析式,及直线与圆、圆与圆的位置关系.圆与圆的位置关系有:相离(外离,内含),相交、相切(外切、内切),直线和圆的位置关系有:相交、相切、相离,所以这样一来,我们在分析过程中不能忽略所有的可能情况.

练习册系列答案
相关题目
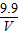 .
.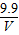 .
.