题目内容
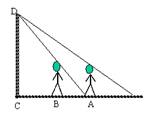
 墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m,小明向墙壁走0.6m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=________m.
墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m,小明向墙壁走0.6m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=________m.
4.27
分析:利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离即可.
解答: 解:如图:
解:如图:
根据题意得:BG=AF=AE=1.6m,AB=0.6m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.2)m,AC=(x+0.6)m,
∴ =
=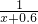 ,
,
解得:x=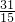 ,y=
,y= ,
,
∴CD= ≈4.27.
≈4.27.
故答案为4.27.
点评:本题考查了相似三角形的应用,解题的关键是根据题意得到相似三角形并利用相似三角形的性质得到比例线段.
分析:利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离即可.
解答:
 解:如图:
解:如图:根据题意得:BG=AF=AE=1.6m,AB=0.6m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.2)m,AC=(x+0.6)m,
∴
 =
=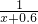 ,
,解得:x=
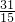 ,y=
,y= ,
,∴CD=
 ≈4.27.
≈4.27.故答案为4.27.
点评:本题考查了相似三角形的应用,解题的关键是根据题意得到相似三角形并利用相似三角形的性质得到比例线段.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
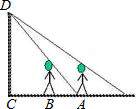 墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m,小明向墙壁走1m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=
墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m,小明向墙壁走1m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=