题目内容
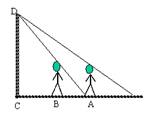
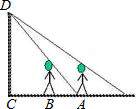 墙壁D处有一盏灯(如图),小明站在A处测得他的影长OA与身长AE相等,都为1.6m,小明向墙壁走1m到B处发现影子刚好落在A点,求灯泡与地面的距离CD.
墙壁D处有一盏灯(如图),小明站在A处测得他的影长OA与身长AE相等,都为1.6m,小明向墙壁走1m到B处发现影子刚好落在A点,求灯泡与地面的距离CD.
分析:利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离即可.
解答: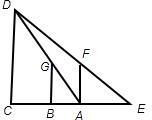 解:如图:
解:如图:
根据题意得:BG=AF=AE=1.6m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.6)m,AC=(x+1)m,
∴
=
,
=
,
解得:x=
,y=
,
∴CD=
m,
∴灯泡与地面的距离为
米.
 解:如图:
解:如图:根据题意得:BG=AF=AE=1.6m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.6)m,AC=(x+1)m,
∴
| 1.6 |
| x+2.6 |
| 1.6 |
| y |
| 1 |
| x+1 |
| 1.6 |
| y |
解得:x=
| 5 |
| 3 |
| 64 |
| 15 |
∴CD=
| 64 |
| 15 |
∴灯泡与地面的距离为
| 64 |
| 15 |
点评:此题主要考查了相似三角形的应用,把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程组是解题关键.

练习册系列答案
相关题目