题目内容
如图(1),有A型、B型、C型三种不同的纸板,其中A形是边长为m的正方形,B型是长为m、宽为n的长方形,C型是边长为n的正方形.由图(2)中四块纸板拼成的正方形的面积关系可以说明(m+n)2=m2+2mn+n2成立.
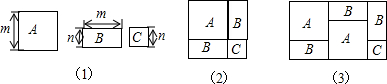
(1)类似地,由图(3)中六块纸板拼成的大长方形的面积关系可以说明的等式是
(2)现有A型纸板2块,B型纸板5块,C型纸板2块,要求紧密且不重叠地拼出一个大长方形,如果纸板最多剩一块,请画出所有可能拼出的大长方形的示意图;类似地,根据所拼出的大长方形的面积关系写出可以说明的等式.
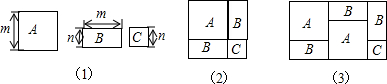
(1)类似地,由图(3)中六块纸板拼成的大长方形的面积关系可以说明的等式是
(m+n)(2m+n)=2m2+3mn+n2
(m+n)(2m+n)=2m2+3mn+n2
.(2)现有A型纸板2块,B型纸板5块,C型纸板2块,要求紧密且不重叠地拼出一个大长方形,如果纸板最多剩一块,请画出所有可能拼出的大长方形的示意图;类似地,根据所拼出的大长方形的面积关系写出可以说明的等式.
分析:(1)六块纸板拼成的大长方形的宽为(m+n)、长为(2m+n),而它由2块A型、3块B型、1块C型组成,所以可以说明的等式是(m+n)(2m+n)=2m2+3mn+n2;
(2)A型纸板2块,B型纸板5块,C型纸板2块不重叠地拼出一个大长方形可得到边长为2m+n与m+2n的长方形;若剩一块C型纸板,可得到边长为2m+2n与m+n的长方形.
(2)A型纸板2块,B型纸板5块,C型纸板2块不重叠地拼出一个大长方形可得到边长为2m+n与m+2n的长方形;若剩一块C型纸板,可得到边长为2m+2n与m+n的长方形.
解答: 解:(1)六块纸板拼成的大长方形的面积关系可以说明的等式为(m+n)(2m+n)=2m2+3mn+n2;
解:(1)六块纸板拼成的大长方形的面积关系可以说明的等式为(m+n)(2m+n)=2m2+3mn+n2;
(2)图(4)中九块纸板拼成的大长方形的面积关系可以说明的等式为(2m+n)(m+2n)=2m2+5mn+2n2;
若剩一块C型纸板,如图(5)中八块纸板拼成的大长方形的面积关系可以说明的等式为(2m+2n)(m+n)=2m2+4mn+2n2.
故答案为(m+n)(2m+n)=2m2+3mn+n2.
 解:(1)六块纸板拼成的大长方形的面积关系可以说明的等式为(m+n)(2m+n)=2m2+3mn+n2;
解:(1)六块纸板拼成的大长方形的面积关系可以说明的等式为(m+n)(2m+n)=2m2+3mn+n2;(2)图(4)中九块纸板拼成的大长方形的面积关系可以说明的等式为(2m+n)(m+2n)=2m2+5mn+2n2;
若剩一块C型纸板,如图(5)中八块纸板拼成的大长方形的面积关系可以说明的等式为(2m+2n)(m+n)=2m2+4mn+2n2.
故答案为(m+n)(2m+n)=2m2+3mn+n2.
点评:本题考查了完全平方公式的几何背景:运用几何直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
有一种规格为165cm×30cm的标准板材,可按如图所示的两种裁法得到规格为60cm×30cm的A型板材与规格为35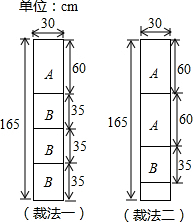 cm×30cm的B型板材.
cm×30cm的B型板材.
(1)某公司装修需要A型板材140张,B型板材215张.现购得标准板材100张,恰好裁完.设按裁法一裁剪的标准板材为x张.
①根据题意,完成以下表格:
②按以上两种裁法的张数来分,共有哪几种裁剪方案?
(2)若装修师傅购买标准板材若干张,按以上两种方法裁剪后,得到A型板材恰为140张,B型板材恰为a张(180<a<200),则购进的标准板材可以是 张.(写出一个即可)
 cm×30cm的B型板材.
cm×30cm的B型板材.(1)某公司装修需要A型板材140张,B型板材215张.现购得标准板材100张,恰好裁完.设按裁法一裁剪的标准板材为x张.
①根据题意,完成以下表格:
| 标准板材裁法一 | 标准板材裁法二 | |
| x(张) | ||
| A型板材(张) | 2(100-x) | |
| B型板材(张) | 3x |
(2)若装修师傅购买标准板材若干张,按以上两种方法裁剪后,得到A型板材恰为140张,B型板材恰为a张(180<a<200),则购进的标准板材可以是
 27、将如图所示的小“L”型的纸片拼成一个大“L”型的图案,有多少种不同的拼图方案试画出其中一种拼图的方案,此时需要多少张小“L”型的纸片.
27、将如图所示的小“L”型的纸片拼成一个大“L”型的图案,有多少种不同的拼图方案试画出其中一种拼图的方案,此时需要多少张小“L”型的纸片.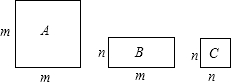 三种不同类型的长方形地砖长度如图所示,若有A型4块,B型4块,C型2块,要拼成一个正方形,则应多余出1块
三种不同类型的长方形地砖长度如图所示,若有A型4块,B型4块,C型2块,要拼成一个正方形,则应多余出1块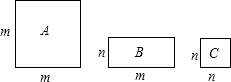 三种不同类型的长方形地砖长度如图所示,若有A型4块,B型4块,C型2块,要拼成一个正方形,则应多余出1块________型地砖,这样的地砖拼法表示了一个两数和的平方的几何意义,这两个数的平方是________(写成两数和的平方的形式)
三种不同类型的长方形地砖长度如图所示,若有A型4块,B型4块,C型2块,要拼成一个正方形,则应多余出1块________型地砖,这样的地砖拼法表示了一个两数和的平方的几何意义,这两个数的平方是________(写成两数和的平方的形式)