题目内容
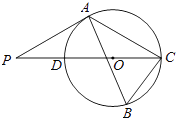
【题目】我们规定:在正方形ABCD中,以正方形的一个顶点A为顶点,且过对角顶点C的抛物线,称为这个正方形的以A为顶点的对角抛物线.
(1)在平面直角坐标系xOy中,点在轴正半轴上,点C在y轴正半轴上.
①如图1,正方形OABC的边长为2,求以O为顶点的对角抛物线;
②如图2,在平面直角坐标系xOy中,正方形OABC的边长为a,其以O为顶点的对角抛物线的解析式为y= ![]() x2 , 求a的值;
x2 , 求a的值;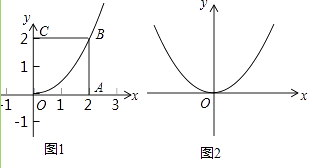
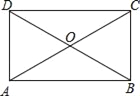
(2)如图3,正方形ABCD的边长为4,且点A的坐标为(3,2),正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q,直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标.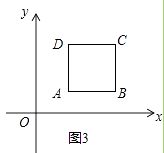
【答案】
(1)
解:①如图1中,设O为顶点的抛物线的解析式为y=ax2,
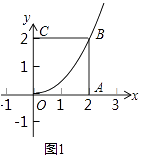
∵过B(2,2),
∴2=4a,
∴a= ![]() ,
,
∴所求的抛物线的解析式为y= ![]() x2.
x2.
②如图2中,设B(a,a).
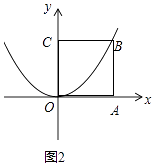
则有a= ![]() a2,解得a=4或0(舍弃),
a2,解得a=4或0(舍弃),
∴B(4,4),
∴OA=4,
∴正方形的边长为4
(2)
解:如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).
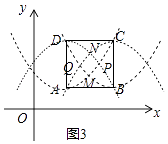
理由:∵正方形ABCD的边长为4,A(3,2),
∴B(7,2),C(7,6),D(3,6),
∴以A为顶点的对角抛物线为y= ![]() (x﹣3)2+2,
(x﹣3)2+2,
以B为顶点的对角抛物线为y= ![]() (x﹣7)2+2,
(x﹣7)2+2,
以C为顶点的对角抛物线为y=﹣ ![]() (x﹣7)2+6,
(x﹣7)2+6,
以D为顶点的对角抛物线为y=﹣ ![]() (x﹣3)2+6,
(x﹣3)2+6,
由 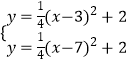 可得M(5,3),
可得M(5,3),
由 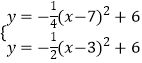 可得N(5,5),
可得N(5,5),
由 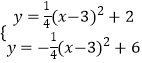 可得P(3+2
可得P(3+2 ![]() ,4),
,4),
由 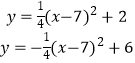 可得Q(7﹣2
可得Q(7﹣2 ![]() ,4),
,4),
∴PM= ![]() ,
,
PN= ![]() ,
,
QN= ![]() ,
,
QM= ![]() ,
,
∴PM=PN=QN=QM,
∴四边形MPNQ是菱形,对角线的交点坐标为(5,5)
【解析】(1)①设O为顶点的抛物线的解析式为y=ax2 , 把B(2,2)代入即可解决问题.②设B(a,a).代入y= ![]() x2求出a即可解决问题.(2)如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).求出A、B、C、D的顶点的对角抛物线,利用方程组求出M、P、N、Q的坐标即可解决问题.
x2求出a即可解决问题.(2)如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).求出A、B、C、D的顶点的对角抛物线,利用方程组求出M、P、N、Q的坐标即可解决问题.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】某仓库本周运进货物件数和运出货物件数如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
运进货物件数 | 5 | a | 5 | 5 | b | 5 | 5 |
运出货物件数 | 12 | 2a | 8 | 0 | b﹣5 | 5 | 10 |
(1)如果用正数表示运进货物件数,负数表示运出货物件数,请你分别表示出周二、周五当天进出货物后变化的量;
(2)若经过一周的时间,仓库货物总量相比上周末库存量减少了5件,求a的值;
(3)若本周运进货物总件数比运出货物件数的一半多15件,本周运进货物总件数比上周减少![]() ,而本周运出货物总件数比上周多
,而本周运出货物总件数比上周多![]() ,这两周内,该仓库货物共增加了3件,求a、b的值.
,这两周内,该仓库货物共增加了3件,求a、b的值.
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):
表示立方米):
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算 | |
例:若某户居民![]() 月份用水
月份用水![]() ,应收水费为
,应收水费为![]() (元).
(元).
请根据上表的内容解答下列问题:
![]() 填空:若该户居民
填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费________元;
,则应收水费________元;
![]() 若该户居民
若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?(用含
),则应收水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
![]() 若该户居民
若该户居民![]() ,
,![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() ,
,![]() 两个月共交水费多少元?(用含
两个月共交水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)