题目内容
（1997•辽宁）方程（x+1）（3x-2）=0的根是
x1=-1，x2=
| 2 |
| 3 |
x1=-1，x2=
．| 2 |
| 3 |
分析：原方程可化为x-1=0或3x-2=0，然后解两个一元一次方程即可．
解答：解：∵（x+1）（3x-2）=0，
∴x+1=0或3x-2=0，
∴x1=-1，x2=
．
故答案为x1=-1，x2=
．
∴x+1=0或3x-2=0，
∴x1=-1，x2=
| 2 |
| 3 |
故答案为x1=-1，x2=
| 2 |
| 3 |
点评：本题考查了解一元二次方程-因式分解法：先把方程右边变形为0，再把方程左边分解为两个一次式的乘积，这样原方程转化为两个一元一次方程，然后解一次方程即可得到一元二次方程的解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
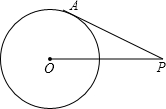（1997•辽宁）如图，PA切⊙O于点A，⊙O的半径为3cm．OP=6cm，则PA=