题目内容
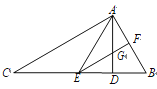
【题目】如图,在△ABC 中,AD 是 BC 边上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB、AD 于点 F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF; ③∠BAE=∠BEA; ④∠B=2∠AEF,其中正确的有( )
A. 4 个B. 3 个C. 2 个D. 1 个
【答案】B
【解析】
利用高线和同角的余角相等,三角形内角和定理即可证明①,再利用等量代换即可得到③
④均是正确的,②缺少条件无法证明.
解:由已知可知∠ADC=∠ADB=90°,
∵∠ACB=∠BAD
∴90°-∠ACB=90°-∠BAD,即∠CAD=∠B,
∵三角形ABC的内角和=∠ACB+∠B+∠BAD+∠CAD=180°,
∴∠CAB=90°,①正确,
∵AE平分∠CAD,EF∥AC,
∴∠CAE=∠EAD=∠AEF,∠C=∠FEB=∠BAD,②错误,
∵∠BAE=∠BAD+∠DAE,∠BEA=∠BEF+∠AEF,
∴∠BAE=∠BEA,③正确,
∵∠B=∠DAC=2∠CAE=2∠AEF,④正确,
综上正确的一共有3个,故选B.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目