题目内容
【题目】如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
(Ⅰ)计算AB的长等于;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明) .
【答案】![]() ;取BC的中点P,在AC上截取AQ=
;取BC的中点P,在AC上截取AQ= ![]() AC,线段PQ即为所求
AC,线段PQ即为所求
【解析】解:(Ⅰ)由图象可知AB= ![]() =
= ![]() .
.
(Ⅱ)设BP=CQ=x,
∵BC= ![]() =
= ![]() ,
,
∴PC= ![]() ﹣x,
﹣x,
在Rt△PCQ中,PQ= ![]() =
= ![]() ,
,
对于函数y=2x2﹣3 ![]() x+
x+ ![]() ,当x=﹣
,当x=﹣ ![]() =
= ![]() 时,y有最小值,此时PQ的值最小,
时,y有最小值,此时PQ的值最小,
此时PC=PB=CQ= ![]() AC.取BC的中点P,在AC上截取AQ=
AC.取BC的中点P,在AC上截取AQ= ![]() AC,图中PQ即为所求.
AC,图中PQ即为所求.

所以答案是:取BC的中点P,在AC上截取AQ= ![]() AC,线段PQ即为所求.
AC,线段PQ即为所求.
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
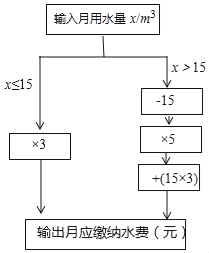
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.