题目内容
如图,已知反比例函数 (
( )与一次函数
)与一次函数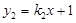 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C.若△OAC的面积为1,且tan∠AOC=2.
轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当 为何值时,反比例函数
为何值时,反比例函数 的值大于一次函数
的值大于一次函数 的值?
的值?

 (
( )与一次函数
)与一次函数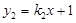 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C.若△OAC的面积为1,且tan∠AOC=2.
轴于点C.若△OAC的面积为1,且tan∠AOC=2.(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当
 为何值时,反比例函数
为何值时,反比例函数 的值大于一次函数
的值大于一次函数 的值?
的值?
(1)y1=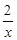 .y2=x+1;(2)B点的坐标为(-2,-1).当0<x<1或x<-2时,y1>y2.
.y2=x+1;(2)B点的坐标为(-2,-1).当0<x<1或x<-2时,y1>y2.
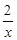 .y2=x+1;(2)B点的坐标为(-2,-1).当0<x<1或x<-2时,y1>y2.
.y2=x+1;(2)B点的坐标为(-2,-1).当0<x<1或x<-2时,y1>y2.试题分析:(1)设OC=m.根据已知条件得,AC=2,则得出A点的坐标,从而得出反比例函数的解析式和一次函数的表达式;
(2)易得出点B的坐标,反比例函数y1的图象在一次函数y2的图象的上方时,即y1大于y2.
(1)在Rt△OAC中,设OC=m.
∵tan∠AOC=
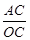 =2,
=2,∴AC=2×OC=2m.
∵S△OAC=
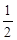 ×OC×AC=
×OC×AC=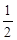 ×m×2m=1,
×m×2m=1,∴m2=1.
∴m=1,m=-1(舍去).
∴m=1,
∴A点的坐标为(1,2).
把A点的坐标代入y1=
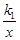 中,得k1=2.
中,得k1=2.∴反比例函数的表达式为y1=
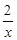 .
.把A点的坐标代入y2=k2x+1中,得k2+1=2,
∴k2=1.
∴一次函数的表达式y2=x+1;
(2)B点的坐标为(-2,-1).
当0<x<1或x<-2时,y1>y2.

练习册系列答案
相关题目
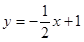 与x轴、y轴分别交于B点、A点,直线
与x轴、y轴分别交于B点、A点,直线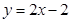 与x轴、y轴分别交于D点、E点,两条直线交于点C,求⊿BCD的外接圆直径的长度。
与x轴、y轴分别交于D点、E点,两条直线交于点C,求⊿BCD的外接圆直径的长度。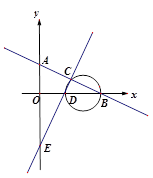

 ,则原方程的根可视为函数y=x+3与y=
,则原方程的根可视为函数y=x+3与y=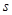 (千米)与时间
(千米)与时间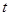 (小时)之间函数关系的大致图象是( )。
(小时)之间函数关系的大致图象是( )。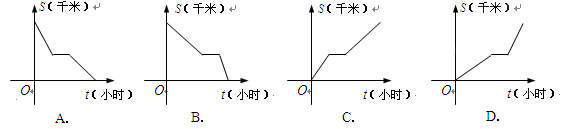
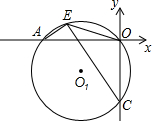
 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合), 的值是否发生变化?( )
的值是否发生变化?( )

 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数
的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数 的表达式.
的表达式. 