题目内容
【题目】如图,在平面直角坐标系xOy中,ABCO的顶点A,B的坐标分别是A(3,0),B(0,2),动点P在直线y=![]() x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.
x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.

【答案】(0,0)或(![]() ,1)或(3﹣
,1)或(3﹣![]() ,
,![]() ).
).
【解析】分析:设P(x,![]() ),⊙P的半径为r,由题意BC⊥y轴,直线OP的解析式y=
),⊙P的半径为r,由题意BC⊥y轴,直线OP的解析式y=![]() ,直线OC的解析式为
,直线OC的解析式为![]() 可知OP⊥OC,分分四种情形讨论即可得出答案.
可知OP⊥OC,分分四种情形讨论即可得出答案.
详解:①当⊙P与BC相切时,∵动点P在直线y=![]() x上,
x上,
∴P与O重合,此时圆心P到BC的距离为OB, ∴P(0,0).
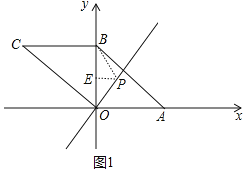
②如图1中,当⊙P与OC相切时,则OP=BP,△OPB是等腰三角形,作PE⊥y轴于E,则EB=EO,易知P的纵坐标为1,可得P(![]() ,1).
,1).
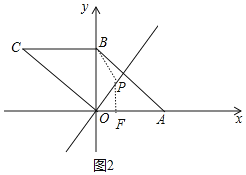
③如图2中,当⊙P与OA相切时,则点P到点B的距离与点P到x轴的距离线段,可得:![]() ,解得x=3+
,解得x=3+![]() 或3-
或3-![]() , ∵x=3+
, ∵x=3+![]() >OA,∴P不会与OA相切,
>OA,∴P不会与OA相切,
∴x=3+![]() 不合题意, ∴p(3-
不合题意, ∴p(3-![]() ,
,![]() ).
).
④如图3中,当⊙P与AB相切时,设线段AB与直线OP的交点为G,此时PB=PG,
∵OP⊥AB,∴∠BGP=∠PBG=90°不成立,∴此种情形,不存在P.

综上所述,满足条件的P的坐标为(0,0)或(![]() ,1)或(3-
,1)或(3-![]() ,
,![]() ).
).

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目








