题目内容
已知两圆半径分别是方程x2-4x+3=0的两根,两圆圆心距为2,则两圆位置关系是( )
| A、外切 | B、相交 | C、内切 | D、外离 |
考点:圆与圆的位置关系,解一元二次方程-因式分解法
专题:
分析:首先解得一元二次方程求得两圆的圆心,然后利用圆心距和两圆的半径之间的关系求解.
解答:解:∵两圆半径的长分别为方程x2-4x+3=0的两根,
∴两圆半径分别为3,1,
又∵两圆的圆心距为2,
∴2=3-1,
∴两圆内切.
故选C.
∴两圆半径分别为3,1,
又∵两圆的圆心距为2,
∴2=3-1,
∴两圆内切.
故选C.
点评:此题考查两圆位置关系的判定方法.根据数量关系与两圆位置关系的对应情况便可直接得出答案.外离,则P>R+r;外切,则P=R+r;相交,则R-r<P<R+r;内切,则P=R-r;内含,则P<R-r.(P表示圆心距,R,r分别表示两圆的半径).

练习册系列答案
相关题目
 如图,下列推理正确的是( )
如图,下列推理正确的是( )| A、∵∠1=∠2,∴AD∥BC |
| B、∵∠3=∠4,∴AB∥CD |
| C、∵∠3=∠5,∴AB∥DC |
| D、∵∠3=∠5,∴AD∥BC |
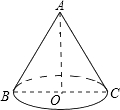 已知圆锥底面半径为4cm,侧面积为32πcm2,设圆锥的母线与高的夹角为θ,如图,则tanθ的值( )
已知圆锥底面半径为4cm,侧面积为32πcm2,设圆锥的母线与高的夹角为θ,如图,则tanθ的值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列选项中正确的是( )
A、
| ||||
B、(-
| ||||
C、(x-
| ||||
| D、平行四边形的对角线相等 |
 如图,在△ABC,∠B=90°,AB=BD=DE=EC,则下列结论中成立的是( )
如图,在△ABC,∠B=90°,AB=BD=DE=EC,则下列结论中成立的是( )| A、△ACD∽△EAD |
| B、△ABD∽△ABC |
| C、△ABE∽△ABC |
| D、△ABE∽△ACD |
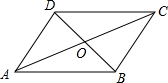 如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC=10cm,BD=8cm,边AB=6cm,则△DOC的周长为
如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC=10cm,BD=8cm,边AB=6cm,则△DOC的周长为 如图,AB•AC=AD•AE,且∠1=∠2,求证:△ABC∽△AED.
如图,AB•AC=AD•AE,且∠1=∠2,求证:△ABC∽△AED.