题目内容
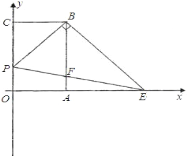
【题目】已知二次函数
的图象与
轴交于
、
两点，与
轴交于点
，
．
（1）若
，函数图象与轴只有一个交点，求
的值；
（2）若
，
，设点的横坐标为
，求证：
；
（3）若
，
，问是否存在实数
，使得
在
时，
随的增大而增大？若存在，求的值；若不存在，请说明理由．
【答案】（1）2；（2）
；（3）不存在．
【解析】
（1）根据条件，抛物线化为：y=﹣x2+bx﹣b+1，由△=0即可解决问题．
（2）根据条件，抛物线化为：y=ax2﹣（a+1）x+1，令y=0求出点B横坐标即可．
（3）不存在．由题意：z=y﹣m2x=x2﹣（c+1+m2）x+c，根据对称轴的位置即可判断．
（1）把点A（1，0）代入y=ax2+bx+c得：a+b+c=0．
∵a=﹣1，∴c=﹣b+1，∴抛物线为y=﹣x2+bx﹣b+1，由题意△=0，∴b2﹣4b+4=0，∴（b﹣2）2=0，∴b=2．
（2）∵b=﹣a﹣c，c=1，∴抛物线为y=ax2﹣（a+1）x+1，令y=0，则有ax2﹣（a+1）x+1=0，∴（x﹣1）（ax﹣1）=0，∴x=1或
．
∵0＜a＜1，∴＞1，∴B点的横坐标为xB＞1．
（3）不存在．理由如下：
∵b=﹣a﹣c，a=1，∴b=﹣1﹣c，∴抛物线为y=x2﹣（c+1）x+c，∴z=y﹣m2x=x2﹣（c+1+m2）x+c．
∵对称轴x=
．
又∵c≥3，m2≥0，∴对称轴x＞0，∴当0＜x＜时，z随x的增大而减小，∴这样的m不存在．
练习册系列答案
相关题目
