题目内容
(本题10分)如图 ,直线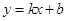 与
与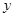 轴的交点坐标为A(0,1),与
轴的交点坐标为A(0,1),与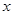 轴的交点坐标为B(-3,0);P、Q分别是
轴的交点坐标为B(-3,0);P、Q分别是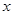 轴和直线AB上的一动
轴和直线AB上的一动
点,在运动过程中,始终保持QA=QP;△APQ沿
直线PQ翻折得到△CPQ,A点的对称点是点C.
(1)求直线AB的解析式.
(2)是否存在点P,使得点C恰好落在直线AB
上?若存在,请求出点P的坐标;若不存在,
请说明理由.
(1)设直线AB的解析式为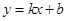 ,则
,则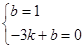 --------------------2分
--------------------2分
解得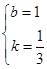 ,即
,即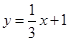 ----------------------------------------------1分
----------------------------------------------1分
(2)分三种情况考虑下
第一种情况(如图甲):设P的坐标为(t,0)
∵△APQ与△CPQ关于直线PQ对称,并且点A,Q,C共线,
 ∴∠AQP=∠CQP=90°,
∴∠AQP=∠CQP=90°,
∵QA=QP,∴QA=QP=QC
即△AQP, △CQP都是等腰直角三角形,
∴△APC是以P为顶角的等腰直角三角形.
根据AAS可以得到△AOP≌△PHC,
∴CH=OP=t,PH=OA=1,
∴点C的坐标为(t+1,t).
∵点C落在直线AB上,
∴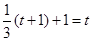 ,解得
,解得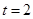 .即P的坐标为(2,0).
--------------------------3分
.即P的坐标为(2,0).
--------------------------3分
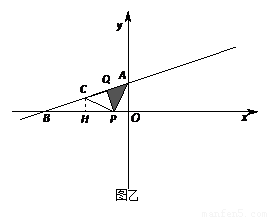 第二种情况(如图乙):设P的坐标为(t,0)
第二种情况(如图乙):设P的坐标为(t,0)
∵△APQ与△CPQ关于直线PQ对称,并且点A,Q,C共线,
∴∠AQP=∠CQP=90°,
∵QA=QP,∴QA=QP=QC,
即△AQP, △CQP都是等腰直角三角形,
∴△APC是以P为顶角的等腰直角三角形.
根据AAS可以得到△AOP≌△PHC,
∴CH=OP=-t,PH=OA=1,
∴点C的坐标为(t-1,-t).
∵点C落在直线AB上,∴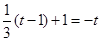 ,解得
,解得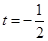 .
.
 即P的坐标为(
即P的坐标为(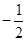 ,0).
-------------------------------------------------3分
,0).
-------------------------------------------------3分
第三种情况(如图丙):
当点P与点B重合时,Q恰好是线段AB的中
点,此时点A关于直线PQ的对称点C与点A重
合,但A,P,Q三点共线,不能构成三角形,
故不符合题意. ------------------------------1分
【解析】略

 53随堂测系列答案
53随堂测系列答案




 的矩形,它的周长为14,面积为10,求下列各式的值:(1)
的矩形,它的周长为14,面积为10,求下列各式的值:(1) (2)
(2) 

