��Ŀ����
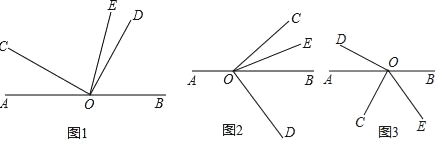
����Ŀ����ֱ֪��AB������O����COD=90�㣬OE����BOC��ƽ���ߣ�
��1����ͼ1������AOC=50��������DOE��
��2����ͼ1������AOC=��������DOE�����ú�����ʽ�ӱ�ʾ��
��3����ͼ1�е���COD�ƶ���O˳ʱ����ת��ͼ2��λ�ã������������䣬��2���еĽ����Ƿ�������˵�����ɣ�
��4����ͼ1�е���COD�ƶ���O��ʱ����ת��ͼ3��λ�ã������������䣬����DOE.���ú�����ʽ�ӱ�ʾ��
���𰸡���1��25�㣻��2��![]() ����3����2���е�
����3����2���е�![]() ���ۻ����������ɼ���������4��180�㩁
���ۻ����������ɼ���������4��180�㩁![]() ��
��
��������
��1����ͼ1������ƽ�ǵĶ���͡�COD=90�㣬�á�AOC+��BOD=90�㣬�Ӷ���ã���BOD=40�㣬�ɽ�ƽ���߶���ã���BOE=![]() ��BOC=65�㣬���ýǵIJ�ɵý��ۣ�
��BOC=65�㣬���ýǵIJ�ɵý��ۣ�
��2��ͬ���ɵã���DOE=![]() ����
����
��3����ͼ2������ƽ�ǵĶ���ã���BOC=180��-�����ɽ�ƽ���߶���ã���EOC=![]() ��BOC=90��-
��BOC=90��-![]() �������ݽǵIJ�ɵã�2���еĽ��ۻ�������
�������ݽǵIJ�ɵã�2���еĽ��ۻ�������
��4��ͬ���ɵã���DOE=��COD+��COE=180��-![]() ����
����
�⣺��1����ͼ1���ߡ�COD=90�㣬
���AOC+��BOD=90�㣬
�ߡ�AOC=50�㣬
���BOD=40�㣬
���BOC=��COD+��BOD=90��+40��=130�㣬
��OEƽ�֡�BOC��
���BOE=![]() ��BOC=65�㣬
��BOC=65�㣬
���DOE=65�㩁40��=25�㣻
��2����ͼ1���ɣ�1��֪����AOC+��BOD=90�㣬
�ߡ�AOC=����
���BOD=90�㩁����
���BOC=��COD+��BOD=90��+90�㩁��=180�㩁����
��OEƽ�֡�BOC��
���BOE=![]() ��BOC =90��
��BOC =90��![]() ����
����
���DOE=��BOE����BOD=90�㩁![]() ������90�㩁����=
������90�㩁����=![]() ����
����
��3������2���еĽ��ۻ������������ǣ�
��ͼ2���ߡ�AOC+��BOC=180�㣬��AOC=����
���BOC=180�㩁����
��OEƽ�֡�BOC��
���EOC=![]() ��BOC=90�㩁
��BOC=90�㩁![]() ����
����
�ߡ�COD=90�㣬
���DOE=��COD����COE=90�㩁��90�㩁![]() ����=
����=![]() ����
����
��4����ͼ3���ߡ�AOC+��BOC=180�㣬��AOC=����
���BOC=180�㩁����
��OEƽ�֡�BOC��
���EOC=![]() ��BOC=90�㩁
��BOC=90�㩁![]() ����
����
�ߡ�COD=90�㣬
���DOE=��COD+��COE=90��+��90�㩁![]() ����=180�㩁
����=180�㩁![]() ����
����