题目内容
 20、如图.已知CE⊥AB,DF⊥AB,点E、F分别为垂足,且AC∥BD.
20、如图.已知CE⊥AB,DF⊥AB,点E、F分别为垂足,且AC∥BD.(1)根据所给的条件,指出△ACE和△BDF具有什么关系,请对你的结论给予说明.
(2)若△ACE和△BDF不全等,请补充一个条件,使这两个三角形全等,并给出证明.
分析:(1)由已知可得出∠AEC=∠BFD=90°,∠A=∠B,所以∠C=∠D,故△ACE∽△BDF;
(2)由(1)若补充一对应边相等,如AE=BF,则两三角形全等.
(2)由(1)若补充一对应边相等,如AE=BF,则两三角形全等.
解答:解:(1)已知CE⊥AB,DF⊥AB,点E、F分别为垂足,且AC∥BD.
∴∠AEC=∠BFD=90°,∠A=∠B,
∴∠C=∠D,
∴△ACE∽△BDF.
(2)若补充AE=BF,使这两个三角形全等.
证明:∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°,
∵AC∥BD,
∴,∠A=∠B,
又AE=BF,
∴△ACE≌△BDF.
∴∠AEC=∠BFD=90°,∠A=∠B,
∴∠C=∠D,
∴△ACE∽△BDF.
(2)若补充AE=BF,使这两个三角形全等.
证明:∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°,
∵AC∥BD,
∴,∠A=∠B,
又AE=BF,
∴△ACE≌△BDF.
点评:此题考查的是全等三角形的判定,解题的关键是由已知条件推出两三角形的对应角相等,得出结论.根据两对应角相等及夹边相等两三角形全等补充条件.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
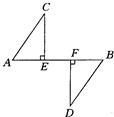 20、如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
20、如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD. 12、如图,已知CE⊥AB,DF⊥AB垂足分别为E、F,AC=BD,要使△AEC≌△BFD只需增加的一个条件是
12、如图,已知CE⊥AB,DF⊥AB垂足分别为E、F,AC=BD,要使△AEC≌△BFD只需增加的一个条件是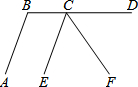 (2013•历下区二模)如图,已知CE∥AB,D为BC延长线上一点,CF平分∠DCE,∠ABD=110°.则∠ECF的度数为( )
(2013•历下区二模)如图,已知CE∥AB,D为BC延长线上一点,CF平分∠DCE,∠ABD=110°.则∠ECF的度数为( )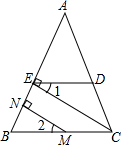 如图,已知CE⊥AB,MN⊥AB,∠1=∠2,求证:∠EDC+∠ACB=180°.
如图,已知CE⊥AB,MN⊥AB,∠1=∠2,求证:∠EDC+∠ACB=180°.