题目内容
【题目】如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为![]() 上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
(1)求证:QN=QF;
(2)若点E到弦MH的距离为1,cos∠Q=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)
证明:如图1,
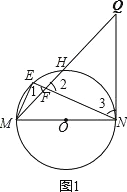
∵ME2=EFEN,
∴![]() =
=![]() .
.
又∵∠MEF=∠MEN,
∴△MEF∽△MEN,
∴∠1=∠EMN.
∵∠1=∠2,∠3=∠EMN,
∴∠2=∠3,
∴QN=QF;
(2)
解:如图2,连接OE交MQ于点G,设⊙O的半径是r.
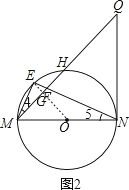
由(1)知,△MEF∽△MEN,则∠4=∠5.
∴![]() =
=![]() .
.
∴OE⊥MQ,
∴EG=1.
∵cos∠Q=![]() ,且∠Q+∠GMO=90°,
,且∠Q+∠GMO=90°,
∴sin∠GMO=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,r=2.5,即⊙O的半径是2.5.
【解析】(1)如图1,通过相似三角形(△MEF∽△MEN)的对应角相等推知,∠1=∠EMN;又由弦切角定理、对顶角相等证得∠2=∠3;最后根据等角对等边证得结论;
(2)如图2,连接OE交MQ于点G,设⊙O的半径是r.根据(1)中的相似三角形的性质证得∠EMF=∠ENM,所以由“圆周角、弧、弦间的关系”推知点E是弧MH的中点,则OE⊥MQ;然后通过解直角△MNE求得cos∠Q=sin∠GMO=![]() =
=![]() , 则可以求r的值.
, 则可以求r的值.
【考点精析】本题主要考查了切线的性质定理和相似三角形的判定与性质的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 3 |
4.4≤x<4.6 | 5 |
4.6≤x<4.8 | 8 |
4.8≤x<5.0 | 17 |
5.0≤x<5.2 | 5 |

(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.