题目内容
(1)如图①、图②,△ABC是等边三角形,点M是边BC上任意一点,N是BA上任意一点,且BN=CM,AM与CN相交于Q,先用量角器测量图①、图②中∠CQM的度数,并用图②证明你的猜想.
猜想:∠CQM=______度.
证明:

(2)如图3,若M是CB延长线上一点,N是BA延长线上一点,仍然满足△ABC为等边三角形,CM=BN,相交于Q,则(1)中猜想还成立吗?若成立,请证明;若不成立,请说明理由.
解:(1)∠CQM为60度,
理由:∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠CAN=60°,
∵BN=CM,
∴AN=BM,
∴△ABM≌△CAN,
∴∠QCA=∠BAM,
∵∠CQM=∠QAC+∠QCA,
∴∠CQM=∠QAC+∠QCA=∠QAC+∠BAM=∠BAC=60°;
(2)成立,
理由:∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=60°,
∵CM=BN,
∴△BNC≌△CMQ,
∴∠N=∠M,
∵∠CQM=∠N+∠NAQ,
∴∠CQA=∠M+∠MAB=∠ABC=60°.
分析:(1)∠CQM为60度,由题不难得△ABM≌△CAN,由∠CQM为△AQM的外角,得∠CQM=∠QAC+∠QCA,因为∠QCA=∠BAM,推出∠CQM=∠QAC+∠QCA=∠QAC+∠BAM=∠BAC=60°;
(2)猜想还成立,根据已知即可推出△BNC≌△CMQ,推出∠N=∠M,由∠CQM=∠N+∠NAQ,通过等量代换即可推出结论.
点评:本题主要考查等边三角形的性质、全等三角形的判定和性质,关键在于求证相关三角形全等.
理由:∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠CAN=60°,
∵BN=CM,
∴AN=BM,
∴△ABM≌△CAN,
∴∠QCA=∠BAM,
∵∠CQM=∠QAC+∠QCA,
∴∠CQM=∠QAC+∠QCA=∠QAC+∠BAM=∠BAC=60°;
(2)成立,

理由:∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=60°,
∵CM=BN,
∴△BNC≌△CMQ,
∴∠N=∠M,
∵∠CQM=∠N+∠NAQ,
∴∠CQA=∠M+∠MAB=∠ABC=60°.
分析:(1)∠CQM为60度,由题不难得△ABM≌△CAN,由∠CQM为△AQM的外角,得∠CQM=∠QAC+∠QCA,因为∠QCA=∠BAM,推出∠CQM=∠QAC+∠QCA=∠QAC+∠BAM=∠BAC=60°;
(2)猜想还成立,根据已知即可推出△BNC≌△CMQ,推出∠N=∠M,由∠CQM=∠N+∠NAQ,通过等量代换即可推出结论.
点评:本题主要考查等边三角形的性质、全等三角形的判定和性质,关键在于求证相关三角形全等.

练习册系列答案
相关题目
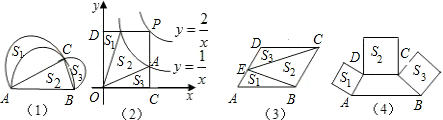
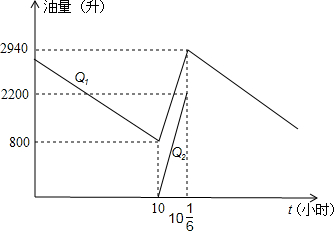 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量;

 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量;