Question

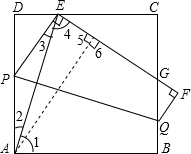
已知正方形ABCD，点P、Q分别是边AD、BC上的两动点，将四边形ABQP沿PQ翻折得到四边形EFQP，点E在线段CD上，EF交BC于G，连接AE．
求证：
（1）EA平分∠DEF；
（2）EC+EG+GC=2AB．

Answer 1

证明：（1）∵四边形ABCD是正方形
∴DC∥AB，∠BAD=90°，
∴∠DEA=∠1，
又由折叠知，PA=PE，∠PEF=∠PAB=90°
∴∠2=∠3，则∠PEF-∠3=∠PAB-∠2，
即∠1=∠4
∴∠DEA=∠4，
即EA平分∠DEF；

（2）在EG上截取EH，使得EH=ED，连接AH、AG
则△ADE≌△AHE（SAS）
∴AD=AH，∠D=∠5
∵四边形ABCD是正方形
∴∠D=∠B=90°，AB=BC=CD=DA
∴AH=AB，且∠5=∠B=90°，则∠6=90°
∵在Rt△AHG和Rt△ABG中

AH=AB AG=AG

∴Rt△AHG≌Rt△ABG（HL）
∴HG=BG，
∴EG=EH+HG=DE+BG，
∴EC+EG+GC=EC+DE+BG+GC=DC+BC=2AB．