题目内容
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知厂家两种球的批发价和商场两种球的零售价如下表,试解答下列问题:
品名 | 厂家批发价(元/个) | 商场零售价(元/个) |
篮球 | 130 | 160 |
排球 | 100 | 120 |
(1)该采购员最多可购进篮球多少个?
(2)若该商场把这100个球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少个?该商场最多可盈利多少元?
【答案】(1)该采购员最多可购进篮球60个;(2) 采购员至少要购篮球58个,该商场最多可盈利2600元.
【解析】试题分析:(1)首先设采购员最多购进篮球x个,排球(100-x)个,列出不等式方程求解;
(2)由题意知篮球利润大于排球,则可推出篮球最多时商场盈利最多.
试题解析:(1)设采购员购进篮球x个,根据题意得:
130x+100(100-x)≤11815,
解得x≤60.5,
因为x为正整数,所以x的最大值是60.
答:采购员最多购进篮球60个;
(2)设至少采购篮球x个,则排球采购(100-x)个,
则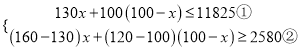
解得:58≤x≤60.8,
篮球的利润大于排球的利润,因此这100个球中,当篮球最多时,商场可盈利最多,
故篮球60个,此时排球40个,商场可盈利(160-130)×60+(120-100)×40=1800+800=2600(元).
所以采购员至少要购篮球58个,该商场最多可盈利2600元.

练习册系列答案
相关题目