Question

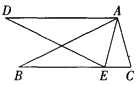
【题目】在梯形ABCD中，AD∥BC，∠ABC=90°，对角线AC、BD相交于点O．下列条件中，不能判断对角线互相垂直的是（ ）
A.∠1=∠4
B.∠1=∠3
C.∠2=∠3
D.OB2+OC2=BC2

Answer 1

【答案】B
【解析】解：A、若∠1=∠4，由∠4+∠2=90°，则∠1+∠2=90°，故本选项符合题意． B、∠1=∠3得不出∠1+∠2=90°，不符合题意，故本选项错误；
C、∠2=∠3，则∠1+∠2=∠1+∠3=90°，故本选项正确．
D、根据勾股定理可得，此选项符合题意，故本选项正确．
故选B．
【考点精析】掌握勾股定理的逆定理和梯形的定义是解答本题的根本，需要知道如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形；一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形．