题目内容
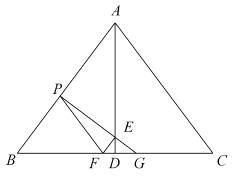
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 是边
是边![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交线段
,交线段![]() 于点
于点![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出定义域;
之间的函数关系式,并写出定义域;
(3)![]() 能否为直角三角形?如果能,求出
能否为直角三角形?如果能,求出![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,定义域为:
,定义域为:![]() ;(3)当BP为
;(3)当BP为![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.
【解析】
(1)根据等腰三角形的性质可得BD=CD=3,通过证明△ABD∽△GBP,可得![]() ,即可得出DG的长度;
,即可得出DG的长度;
(2)根据相似三角形的性质可得![]() ,
,![]() ,根据三角形的面积公式即可表达出;
,根据三角形的面积公式即可表达出;
(3)分EF⊥PG,EF⊥PF两种情况,根据相似三角形的性质即可求出BP的长度.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴BD=CD=3
在Rt△ABD中,![]() ,
,
∵∠B=∠B,∠ADB=∠BPG=90°,
∴△ABD∽△GBP
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]()
(2)∵PF∥AC
∴△BFP∽△BCA
∴![]()
即![]()
∴![]()
∴![]() ,
,
∵∠DGE+∠DEG=∠DGE+∠ABD,
∴∠DEG=∠ABD,∠ADG=∠ADB=90°,
∴△DEG∽△DBA
∴![]() ,
,
∴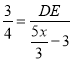 ,
,
整理得:![]() ,
,
∴![]()
定义域为:![]()
(3)若EF⊥PG时,
∵EF⊥PG,ED⊥FG,
∴∠FED+∠DEG=90°,∠FED+∠EFD=90°,
∴∠DEG=∠EFD,且∠EDF=∠EDG,
∴△EFD∽△GDE,
∴![]()
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
若EF⊥PF,
∴∠PFB+∠EFD=90°,且∠PFB=∠ACB,∠ACB+∠DAC=90°,
∴∠EFD=∠DAC,且∠EDF=∠ADC=90°,
∴△EDF∽△CDA
∴![]()
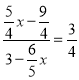 ,
,
解得:![]() ,
,
综上所述,当BP为![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.

练习册系列答案
相关题目