题目内容
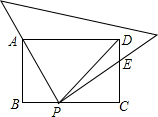如图矩形ABCD中，DP平分∠ADC交BC于P点，将一个直角三角板的直角顶点放在P点处，且使它的一条直角边过A点，另一条直角边交CD于E．找出图中与PA相等的线段．并说明理由．
解：图中与PA相等的线段是PE．理由如下：
由DP平分∠ADC可得∠ADP=∠PDC=45°，
又由AD∥BC可得∠ADP=∠DPC，从而得到∠PDC=∠DPC，所以PC=DC．
又因为AB=DC，所以AB=PC．
由于直角三角板的直角顶点放在点P处，所以∠APE=90°．
从而∠APB+∠EPC=90°．
∵∠EPC+∠PEC=90°．
∴∠APB=∠PEC．
在△PAB和△EPC中，
因为∠B=∠C=90°，AB=PC，∠APB=∠PEC，
所以△PAB≌△EPC（AAS），
从而可得PE=PA．
分析：可由∠B=∠C=90°，AB=PC，∠APB=∠PEC，证得△ABP≌△PCE，所以PA=PE．
点评：本题把角平分线置于矩形的背景之中，与平行线组合使用，沟通了角与角之间的关系．由于角平分线、平行线都具有转化角的作用，在两者共存的图形中常会出现等腰三角形，所以命题者常将两者组合，设计出精彩纷呈的题目．
由DP平分∠ADC可得∠ADP=∠PDC=45°，
又由AD∥BC可得∠ADP=∠DPC，从而得到∠PDC=∠DPC，所以PC=DC．
又因为AB=DC，所以AB=PC．
由于直角三角板的直角顶点放在点P处，所以∠APE=90°．
从而∠APB+∠EPC=90°．
∵∠EPC+∠PEC=90°．
∴∠APB=∠PEC．
在△PAB和△EPC中，
因为∠B=∠C=90°，AB=PC，∠APB=∠PEC，
所以△PAB≌△EPC（AAS），
从而可得PE=PA．
分析：可由∠B=∠C=90°，AB=PC，∠APB=∠PEC，证得△ABP≌△PCE，所以PA=PE．
点评：本题把角平分线置于矩形的背景之中，与平行线组合使用，沟通了角与角之间的关系．由于角平分线、平行线都具有转化角的作用，在两者共存的图形中常会出现等腰三角形，所以命题者常将两者组合，设计出精彩纷呈的题目．
练习册系列答案
相关题目
14、如图矩形ABCD中BC=8，AB=4，将矩形纸片沿对角线对折，使C点落在F处，BC与AD边交于点E，则下列四个结论中：
如图矩形ABCD中，E为BC上一点，DF⊥AE于F．
29、如图矩形ABCD中，DP平分∠ADC交BC于P点，将一个直角三角板的直角顶点放在P点处，且使它的一条直角边过A点，另一条直角边交CD于E．找出图中与PA相等的线段．并说明理由．
如图矩形ABCD中，过A，B两点的⊙O切CD于E，交BC于F，AH⊥BE于H，连接EF．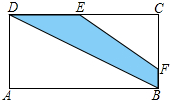
如图矩形ABCD中，AB=8cm，CB=4cm，E是DC的中点，BF=