题目内容
 如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.
如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.(1)求证:∠CEF=∠BAH;
(2)若BC=2CE=6,求BF的长.
分析:(1)根据弦切角定理得到∠FEC=∠EBC,根据等角的余角相等得到∠BAH=∠EBC,从而根据等量代换进行证明;
(2)根据切割线定理EC2=CF•BC,计算得到CF的长,再进一步计算BF的长.
(2)根据切割线定理EC2=CF•BC,计算得到CF的长,再进一步计算BF的长.
解答:(1)证明:∵CD切⊙O于E,
∴∠FEC=∠EBC.
∵ABCD为矩形,
∴∠ABC=90°,
∴∠ABE+∠EBC=90°.
∵AH⊥BE,
∴∠BAH=∠EBC,
∴∠FEC=∠BAH.
(2)解:∵EC切⊙O于E,
∴EC2=CF•BC.
∵BC=2CE=6,
∴32=CF•6,
∴CF=
.
∴BF=BC-CF=6-
=
.
∴∠FEC=∠EBC.
∵ABCD为矩形,
∴∠ABC=90°,
∴∠ABE+∠EBC=90°.
∵AH⊥BE,
∴∠BAH=∠EBC,
∴∠FEC=∠BAH.
(2)解:∵EC切⊙O于E,
∴EC2=CF•BC.
∵BC=2CE=6,
∴32=CF•6,
∴CF=
| 3 |
| 2 |
∴BF=BC-CF=6-
| 3 |
| 2 |
| 9 |
| 2 |
点评:综合运用了弦切角定理、切割线定理以及等角的余角相等的性质.

练习册系列答案
相关题目
 14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中:
14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中: 如图矩形ABCD中,E为BC上一点,DF⊥AE于F.
如图矩形ABCD中,E为BC上一点,DF⊥AE于F. 29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由.
29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由.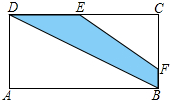 如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=
如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=