题目内容
【题目】《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短.横之不出四尺,纵之不出二尺,斜之适出注.问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰 好能出去.解决下列问题: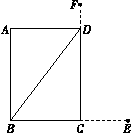
(1)示意图中,线段CE的长为尺,线段DF的长为尺;
(2)求户斜多长.
【答案】
(1)4;2
(2)
解:设户斜x尺
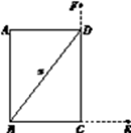
图2
则图2中BD=x,
![]() ,(x>4)
,(x>4)
![]() .(x>2)
.(x>2)
又在Rt△BCD中, ![]() ,
,
由勾股定理得 ![]() .
.
所以 ![]() .
.
整理,得 ![]() .
.
因式分解,得 ![]() .
.
解得 ![]() ,
, ![]() .
.
因为 x>4 且 x>2,所以 ![]() 舍去,
舍去,
∴x ![]() .
.
答:户斜为10尺
【解析】(1)依题可得CE=4,DF=2.
(2)设图2中BD=x,则BC=BECE=x4 (x>4);CD=CFDF=x2 (x>2);在Rt△BCD中, 由勾股定理得 BC2+CD2=BD2 ;即
(x4)2+(x2)2=x2 .解之即可。

练习册系列答案
相关题目