题目内容
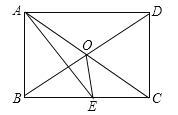
【题目】如图所示,矩形ABCD中AE平分∠BAD交BC于E, ∠CAE=15°,则下面的结论:①△ODC是等边三角形; ②BC=2AB; ③∠AOE=135°; ④![]() ,其中正确结论有( )
,其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=OC,OD=OB,AC=BD,∴OA=OD=OC=OB.∵AE平分∠BAD,∴∠DAE=45°.∵∠CAE=15°,∴∠DAC=30°.∵OA=OD,∴∠ODA=∠DAC=30°,∴∠DOC=60°.∵OD=OC,∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,∴∠DAC=∠ACB=30°,∴AC=2AB.∵AC>BC,∴2AB>BC,∴②错误;
∵AD∥BC,∴∠DBC=∠ADB=30°.∵AE平分∠DAB,∠DAB=90°,∴∠DAE=∠BAE=45°.∵AD∥BC,∴∠DAE=∠AEB,∴∠AEB=∠BAE,∴AB=BE.∵四边形ABCD是矩形,∴∠DOC=60°,DC=AB.∵△DOC是等边三角形,∴DC=OD,∴BE=BO,∴∠BOE=∠BEO=![]() (180°﹣∠OBE)=75°.∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;
(180°﹣∠OBE)=75°.∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,∴根据等底等高的三角形面积相等得出S△AOE=SCOE,∴④正确.
故选C.

练习册系列答案
相关题目